2.26. Адрэзак [0,
a] падзелены
на n роўных частак. На
кожнай частцы як на дыяметры пабудавана паўакружына. Запішыце паслядоўнасць (![]() ) даўжыняў
крывых, складзеных з гэтых паўакружынаў.
) даўжыняў
крывых, складзеных з гэтых паўакружынаў.
2.27. У прамавугольным трохвугольніку, катэты якога роўныя адпаведна a і b, гіпатэнуза падзелена на n роўных частак. З пунктаў падзелу праведзены прамыя, паралельныя катэтам. Пры гэтым атрымліва-ецца ламаная. Знайдзіце паслядоўнасць даўжыняў гэтых ламаных.
2.28. У роўнастаронні трохвугольнік са стараной а
умежана акружына, да якой праведзена датычная, паралельная аснове. Гэтая
датычная зноў адсякае правільны трохвугольнік, у які ўмежана другая акружына
і г. д. Запішыце агульны элемент паслядоўнасці радыусаў (![]() ) акружынаў,
пабудаваных такім чынам.
) акружынаў,
пабудаваных такім чынам.
2.29.
Знайдзіце формулу
агульнага элемента паслядоўнасцяў, зададзеных рэкурэнтным спосабам : 1) ![]() ,
, ![]() ;
2)
;
2) ![]() ,
, ![]() ,
, ![]() ; 3)
; 3) ![]() ,
, ![]() ,
, ![]() .
.
2.30. Пакажыце, што для паслядоўнасці Фібаначы 1, 1,
2, 3, 5, 8, 13, ... або ![]() ,
,
![]()
![]() , n
, n![]() , формула
агульнага элемента мае выгляд:
, формула
агульнага элемента мае выгляд: ![]() .
.
2.31. 1) Дакажыце сцверджанне Эўкліда, што простыя лікі, размешчаныя ў парадку нарастання, утвараюць бясконцую паслядоўнасць. 2) Паспрабуйце атрымаць формулу агульнага элемента гэтай паслядоўнасці.
2.32. Дайце азначэнне абмежаванай паслядоўнасці (абмежаванай зверху, абмежаванай знізу). Якая геаметрычная інтэрпрэтацыя гэтага азначэння?
2.33. Прывядзіце азначэнне ў дадатным сэнсе неабмежаванай паслядоўнасці. Які геаметрычны сэнс гэтага азначэння?
2.34.
Вызначце, якія з прыведзеных
ніжэй паслядоўнасцяў
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) 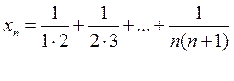 ; 6)
; 6) ![]() ; 7)
; 7) ![]() а) абмежаваныя зверху, б) абмежаваныя знізу?
а) абмежаваныя зверху, б) абмежаваныя знізу?
2.35.
Няхай паслядоўнасць (![]() ) абмежаваная.
Ці заўсёды абмежаваная паслядоўнасць (
) абмежаваная.
Ці заўсёды абмежаваная паслядоўнасць (![]() ), калі:
1)
), калі:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ?
?
2.36. Зададзена неабмежаваная паслядоўнасць (![]() ). Ці заўсёды неабмежаваная
паслядоўнасць (
). Ці заўсёды неабмежаваная
паслядоўнасць (![]() ),
пададзеная ў задачы 2.35?
),
пададзеная ў задачы 2.35?
2.37. Дакажыце, што з абмежаванасці паслядоўнасцяў (![]() ) і (
) і (![]() ) вынікае
абмежаванасць іх сумы і здабытку.
) вынікае
абмежаванасць іх сумы і здабытку.
2.38. Няхай паслядоўнасці (![]() ) і (
) і (![]() ) абмежаваныя,
прычым
) абмежаваныя,
прычым ![]() . Ці заўсёды
паслядоўнасць (
. Ці заўсёды
паслядоўнасць (![]() )
таксама абмежаваная ?
)
таксама абмежаваная ?
2.39.
Дакажыце
неабмежаванасць паслядоўнасцяў:
1) ![]() ; 2)
; 2) 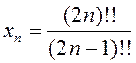 ; 3)
; 3) ![]() ;
4)
;
4) ![]() ; 5)
; 5) ![]() .
.
2.40.
Дакажыце, што
наступныя паслядоўнасці абмежаваныя: 1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() .
.
2.41. Пакажыце, што калі паслядоўнасць (![]() ), дзе
), дзе 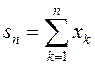 , абмежаваная,
то і паслядоўнасць (
, абмежаваная,
то і паслядоўнасць (![]() ) абмежаваная.
Ці праўдзівае адваротнае сцверджанне?
) абмежаваная.
Ці праўдзівае адваротнае сцверджанне?
2.42. Знайдзіце дакладныя верхнюю і ніжнюю межы
наступных паслядоўнасцяў: 1) ![]() ; 2)
; 2) ![]() .
.
2.43. Вядома, што ![]() , а
, а ![]() . Знайдзіце
дакладныя верхнюю і ніжнюю межы паслядоўнасці (
. Знайдзіце
дакладныя верхнюю і ніжнюю межы паслядоўнасці (![]() ), калі
), калі ![]()
Лік ![]() называецца лімітампаслядоўнасці
называецца лімітампаслядоўнасці ![]() (абазначэнне:
(абазначэнне: ![]() або
або ![]() ), калі
), калі ![]() > 0
> 0 ![]() :
: ![]()
![]() >
> ![]() <
< ![]() . Паслядоў-насць, якая мае ліміт, называецца збежнай,
у адваротным выпадку – разбежнай. Паслядоўнасць (
. Паслядоў-насць, якая мае ліміт, называецца збежнай,
у адваротным выпадку – разбежнай. Паслядоўнасць (![]() ) называюць бясконца
вялікай, (абазначэнне:
) называюць бясконца
вялікай, (абазначэнне: ![]() ), калі
), калі ![]() > 0
> 0 ![]() :
: ![]() >
>
![]() >
>![]() .
.
Тэарэма 1.
Няхай ![]() ,
, ![]() . Тады
1)
. Тады
1) ![]() ; 2)
; 2) ![]()
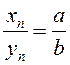 , (
, (![]() ); 3)
); 3) ![]() .
.
Тэарэма 2. (пра сціснутую паслядоўнасць). Калі, пачынаючы з некаторага нумару, ![]() і
і
![]() =
= ![]() = а , то
= а , то
![]() .
.
Тэарэма 3. Калі паслядоўнасць (![]() ) манатонная і
абмежаваная, то яна збежная.
) манатонная і
абмежаваная, то яна збежная.
Лік e: 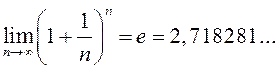 .
.
Крытэр Кашы. Для
таго каб паслядоўнасць ![]() збягалася,
неабходна і дастаткова, каб яна была фундаментальнай, г. зн.
збягалася,
неабходна і дастаткова, каб яна была фундаментальнай, г. зн. ![]()
![]() :
: ![]() ,
, ![]() .
.
►Разгледзім 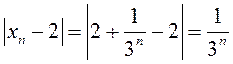 .
У адпаведнасці з азначэннем ліміту мы павінны для адвольнага
.
У адпаведнасці з азначэннем ліміту мы павінны для адвольнага ![]() знайсці
знайсці ![]() , каб
, каб ![]() праўдзілася
няроўнасць
праўдзілася
няроўнасць ![]() Калі развязаць
гэтую няроўнасць у дачыненні да
Калі развязаць
гэтую няроўнасць у дачыненні да ![]() ,
то атрымаем
,
то атрымаем ![]() , г.зн. , што ў
якасці
, г.зн. , што ў
якасці ![]() можна ўзяць
можна ўзяць ![]() Такім чынам,
Такім чынам, ![]()
![]() :
: ![]() , што і патрабавалася.
◄
, што і патрабавалася.
◄
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.