Прыклад 2. Знайсці ![]() .
.
►На гэтым прыкладзе мы праілюструем выкарыстанне
непарыўнасці пры знаходжанні лімітаў. Паколькі ![]() і
і ![]() (грунтоўны
ліміт), то, выкарыстоўваючы непарыўнасць функцыі
(грунтоўны
ліміт), то, выкарыстоўваючы непарыўнасць функцыі ![]() у пункце
у пункце ![]() , маем права
памяняць месцамі сімвалы
, маем права
памяняць месцамі сімвалы ![]() і
і
![]() Атрымаем:
Атрымаем: ![]() .◄
.◄
Заўважым, што знаходжанне гэтага ліміту без скарыстання непарыўнасці лагарыфмічнай функцыі прыводзіць да складаных выкладак.
Прыклад
3. Даказаць раўнамерную
непарыўнасць на адрэзку ![]() функцыі
функцыі
![]() .
.
►Заўважым, па-першае, што раўнамерная непарыўнасць гэтай функ-цыі
вынікае з тэарэмы Кантара і непарыўнасці ![]() на адрэзку
на адрэзку ![]() . Мы правядзем
доказ, карыстаючыся толькі азначэннем раўнамернай непарыўнасці. Для гэтага
возьмем любое
. Мы правядзем
доказ, карыстаючыся толькі азначэннем раўнамернай непарыўнасці. Для гэтага
возьмем любое ![]() і
разгледзім адвольныя пункты
і
разгледзім адвольныя пункты ![]() .
Маем:
.
Маем:
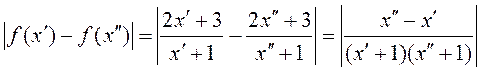 . Паколькі
. Паколькі ![]() , то
, то ![]() і
і ![]() , а таму
, а таму ![]() . З апошняй
няроў-насці вынікае, што
. З апошняй
няроў-насці вынікае, што ![]() >0
дастаткова ўзяць
>0
дастаткова ўзяць ![]() , каб
, каб
![]() выкон-валася
няроўнасць
выкон-валася
няроўнасць ![]() . А гэта і
азначае, што
. А гэта і
азначае, што ![]() раўнамерна
непарыўная на
раўнамерна
непарыўная на ![]() .◄
.◄
2.131. Сфармулюйце азначэнне непарыўнасці функцыі ![]() у пункце
у пункце ![]() , карыстаючыся
азначэннем ліміту функцыі паводле Гайнэ.
, карыстаючыся
азначэннем ліміту функцыі паводле Гайнэ.
2.132. Няхай функцыя ![]() вызначана
ў некаторым ваколлі пункта
вызначана
ў некаторым ваколлі пункта ![]() .
Сфармулюйце ў дадатным сэнсе сцверджанне, што
.
Сфармулюйце ў дадатным сэнсе сцверджанне, што ![]() не з’яўляецца
непарыўнай у пункце
не з’яўляецца
непарыўнай у пункце ![]() .
.
2.133. Карыстаючыся азначэннем Кашы, дакажыце непарыўнасць
функцыі ![]() у кожным
пункце
у кожным
пункце ![]() , калі:
1)
, калі:
1) ![]() 2)
2) ![]() 3)
3) ![]() 4)
4) ![]() .
.
2.134. Дакажыце, што з непарыўнасці функцыі ![]() у пункце
у пункце ![]() вынікае
непарыўнасць у гэтым пункце функцыі
вынікае
непарыўнасць у гэтым пункце функцыі ![]() .
.
2.135.
Даследуйце на непарыўнасць,
знайдзіце пункты разрыву і пабу-дуйце графікі наступных функцый:
1) 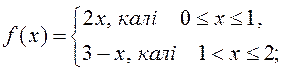 ; 2)
; 2) 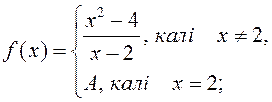 ;
3)
;
3) ![]() 4)
4) ![]() .
.
2.136.
Вызначце тып пунктаў
разрыву функцыі ![]() ,
калі:
1)
,
калі:
1) ![]() ; 2)
; 2) 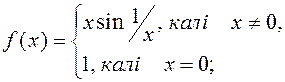 3)
3) 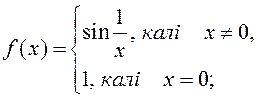 4)
4) ![]() 5)
5) ![]() 6)
6) 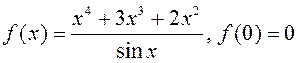 ; 7)
; 7) 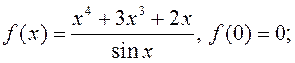 8)
8) 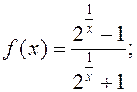 ; 9)
; 9) 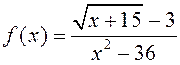 .
.
2.137.
Карыстаючыся
непарыўнасцю элементарных функцый, дакажыце: 1) 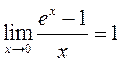 ; 2)
; 2) ![]() ; 3)
; 3) ![]() ;
4)
;
4) 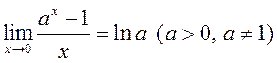 ; 5)
; 5) 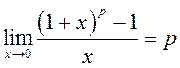 .
.
2.138.
Як патрэбна
давызначыць функцыю ![]() у
пункце
у
пункце ![]() , каб яна была
непарыўнай у гэтым пункце, калі: 1)
, каб яна была
непарыўнай у гэтым пункце, калі: 1) 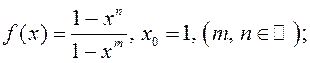 2)
2) ![]() 3)
3) 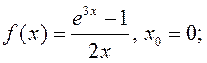 4)
4) 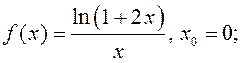 5)
5) 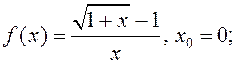 6)
6) ![]() 7)
7) ![]() ?
?
2.139.
Няхай функцыя ![]() непарыўная ў
пункце
непарыўная ў
пункце ![]() і
і 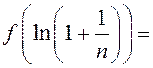
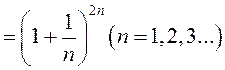 . Знайдзіце
. Знайдзіце ![]() .
.
2.140.
Няхай функцыя ![]() непарыўная ў
пункце
непарыўная ў
пункце ![]() і
і 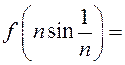
![]() . Знайдзіце
. Знайдзіце ![]() .
.
2.141. Дакажыце, што функцыя Дырыхле з’яўляецца ўсюды разрыўнай.
2.142.
Ці мае функцыя
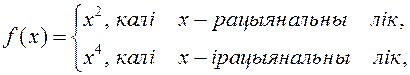 пункты непарыўнасці? Колькі такіх пунктаў?
пункты непарыўнасці? Колькі такіх пунктаў?
2.143. Пабудуйце дзве функцыі, якія маюць разрыў у
пункце ![]() , а іх сума і
здабытак непарыўныя ў гэтым пункце.
, а іх сума і
здабытак непарыўныя ў гэтым пункце.
2.144. Дакажыце, што калі сума дзвюх разрыўных у
пункце ![]() функцый
з’яўляецца непарыўнай у гэтым пункце, то абедзве функцыі маюць у пункце
функцый
з’яўляецца непарыўнай у гэтым пункце, то абедзве функцыі маюць у пункце ![]() разрыў аднаго
і таго ж тыпу. Ці выконваецца аналагічнае сцверджанне для здабытку дзвюх
функцый?
разрыў аднаго
і таго ж тыпу. Ці выконваецца аналагічнае сцверджанне для здабытку дзвюх
функцый?
2.145. Ці могуць дзве непарыўныя на адрэзку ![]() функцыі
адрознівацца толькі ў адным пункце гэтага адрэзка?
функцыі
адрознівацца толькі ў адным пункце гэтага адрэзка?
2.146. Дакажыце, што калі функцыі ![]() і
і ![]() непарыўныя на
непарыўныя на ![]() і ў рацыянальных
пунктах гэтага адрэзка іх значэнні супадаюць, то
і ў рацыянальных
пунктах гэтага адрэзка іх значэнні супадаюць, то ![]() для ўсіх
для ўсіх ![]() .
.
2.147.
Даследуйце на
непарыўнасць і пабудуйце графікі функцый ![]() , калі:
1)
, калі:
1) ![]() ; 2)
; 2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() .
.
2.148. Падайце прыклад функцыі, непарыўнай на
інтэрвале ![]() , якая
неабмежаваная на ім: а) зверху; б) знізу; в) зверху
і знізу.
, якая
неабмежаваная на ім: а) зверху; б) знізу; в) зверху
і знізу.
2.149.
Пабудуйце прыклад функцыі,
вызначанай на адрэзку ![]() , і
не аб-межаванай на гэтым адрэзку: а) зверху; б) знізу.
Ці можа такая функцыя быць непарыўнай на
, і
не аб-межаванай на гэтым адрэзку: а) зверху; б) знізу.
Ці можа такая функцыя быць непарыўнай на ![]() ?
?
2.150. Падайце прыклад абмежаванай і непарыўнай на
інтэрвале ![]() функцыі, якая
на гэтым інтэрвале: а) не дасягае сваёй дакладнай верхняй мяжы
функцыі, якая
на гэтым інтэрвале: а) не дасягае сваёй дакладнай верхняй мяжы ![]() , але дасягае
дакладнай ніжняй мяжы
, але дасягае
дакладнай ніжняй мяжы ![]() ;
б) дасягае
;
б) дасягае ![]() , але
не дасягае
, але
не дасягае ![]() в) не
дасягае
в) не
дасягае ![]() і
і ![]()
2.151.
Знайдзіце дакладныя
межы функцыі ![]() на мностве
на мностве ![]() , калі:
1)
, калі:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.