|
1) |
7) |
|
2) |
8) |
|
3) |
9) |
|
4) |
10) |
|
5) |
11) |
|
6) |
12) |
2.61.
Дакажыце, што паслядоўнасць 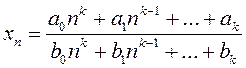 збягаецца да
ліміту
збягаецца да
ліміту ![]() , калі
, калі ![]() .
.
2.62.
Знайдзіце ліміты наступных ірацыянальных
выразаў, выкарыстоў-ваючы прыём перавядзення ірацыянальнасці з назоўніка ў
лічнік або з лічніка ў назоўнік:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) 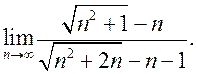
2.63.
Няхай паслядоўнасць ![]() збягаецца, а
паслядоўнасць
збягаецца, а
паслядоўнасць ![]() разбя-гаецца.
1) Дакажыце, што іх сума (
разбя-гаецца.
1) Дакажыце, што іх сума (![]() ) будзе
разбягацца.
2) Што можна сцвярджаць пра збежнасць паслядоўнасці
) будзе
разбягацца.
2) Што можна сцвярджаць пра збежнасць паслядоўнасці ![]() ? Прывядзіце
адпаведныя прыклады.
? Прывядзіце
адпаведныя прыклады.
2.64.
Прывядзіце прыклады разбежных паслядоўнасцяў (![]() ) і (
) і (![]() ), для якіх збягаецца
паслядоўнасць:
1)
), для якіх збягаецца
паслядоўнасць:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() .
.
2.65.
1) Дакажыце,
што 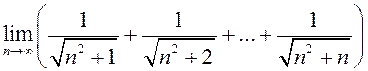 =1.
2) Чаму пры вылічэнні гэтага ліміту нельга карыстацца тэарэмай пра
ліміт сумы паслядоўнасцяў г. зн.
=1.
2) Чаму пры вылічэнні гэтага ліміту нельга карыстацца тэарэмай пра
ліміт сумы паслядоўнасцяў г. зн.
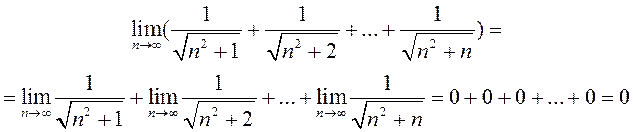 ?
?
2.66.
1) Дакажыце,
што 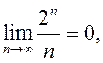 выкарыстоўваючы
няроўнасць
выкарыстоўваючы
няроўнасць 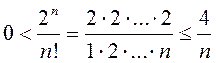 . 2) Абагульніце
атрыманы вынік, устанавіў-шы, што
. 2) Абагульніце
атрыманы вынік, устанавіў-шы, што 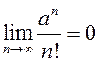 для
адвольнага
для
адвольнага ![]() .
.
2.67.
Скарыстаўшы вынік папярэдняй задачы, дакажыце,
што
![]()
2.68.
Устанавіце праўдзівасць наступных роўнасцяў:
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) 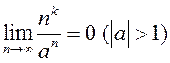 .
.
2.69.
Знайдзіце ліміты
паслядоўнасцяў ![]() ,
калі: 1)
,
калі: 1) ![]() ; 2)
; 2) 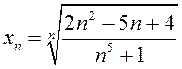 ; 3)
; 3) ![]() , дзе
, дзе ![]() ёсць
мнагасклад ступені
ёсць
мнагасклад ступені ![]() ,
прычым
,
прычым ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() дзе
дзе ![]() дадатныя лікі; 7)
дадатныя лікі; 7) 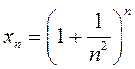 ; 8)
; 8) 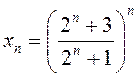 .
.
2.70.
1) Карыстаючыся
тэарэмай пра існаванне ліміту манатоннай пасля-доўнасці, дакажыце збежнасць
паслядоўнасці ![]() .
2) Знайдзіце ліміт гэтай паслядоўнасці, зыходзячы з рэкурэнтнага
судачынення
.
2) Знайдзіце ліміт гэтай паслядоўнасці, зыходзячы з рэкурэнтнага
судачынення ![]() .
.
2.71.
Шляхам, апісаным у задачы 2.70, спачатку
ўстанавіце збежнасць, а потым знайдзіце ліміт паслядоўнасцяў:
1) 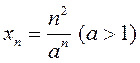 ; 2)
; 2) 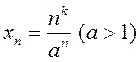 ; 3)
; 3) 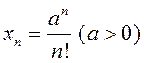 ; 4)
; 4) ![]() ; 5)
; 5) ![]() .
.
2.72.
Праверце, што метад знаходжання ![]() шляхам
пераходу да ліміту ў рэкурэнтным судачыненні, як гэта рабілася ў папярэдняй
задачы, не заўсёды вядзе да мэты. Разгледзьце прыклад:
шляхам
пераходу да ліміту ў рэкурэнтным судачыненні, як гэта рабілася ў папярэдняй
задачы, не заўсёды вядзе да мэты. Разгледзьце прыклад:
![]()
2.73.
Дакажыце збежнасць наступных манатонных
паслядоўнасцяў: 1) ![]() ;
2)
;
2) ![]() ;
3)
;
3) ![]() ; 4)
; 4) ![]() ;
5)
;
5) ![]() ; 6)
; 6) ![]() дзе
дзе![]()
![]() абмежаваная
паслядоўнасць з дадатнымі элементамі.
абмежаваная
паслядоўнасць з дадатнымі элементамі.
2.74.
Знайдзіце:
1)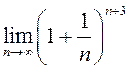 ; 2)
; 2) 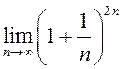 ; 3)
; 3) 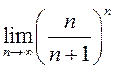 ; 4)
; 4) 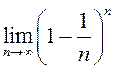 .
.
2.75.
Дакажыце, што паслядоўнасць ![]() з’яўляецца
спадальнай і
з’яўляецца
спадальнай і ![]() (адзначым,
што паслядоўнасць
(адзначым,
што паслядоўнасць ![]() нарастае
).
нарастае
).
2.76.
Дакажыце, што калі ![]() , то любая
падпаслядоўнасць (
, то любая
падпаслядоўнасць (![]() ) таксама
збягаецца да
) таксама
збягаецца да ![]() . Карыстаючыся
даказаным сцверджаннем, пакажыце, што:
1)
. Карыстаючыся
даказаным сцверджаннем, пакажыце, што:
1) 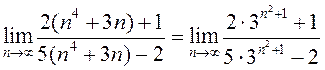 ; 2)
; 2) ![]() .
.
2.77.
Дакажыце раўназначнасць наступных азначэнняў:
1) Лік ![]() называецца
лімітавым пунктам (частковым лімітам) паслядоўнасці
называецца
лімітавым пунктам (частковым лімітам) паслядоўнасці![]() , калі існуе
падпаслядоўнасць
, калі існуе
падпаслядоўнасць![]() ,
збежная да
,
збежная да ![]() .
2) Лік
.
2) Лік ![]() называецца
лімітавым пунктам паслядоўнасці
называецца
лімітавым пунктам паслядоўнасці ![]() , калі ў адвольнай
, калі ў адвольнай
![]()
![]() акрузе пункта
акрузе пункта ![]() знаходзіцца бясконца
многа элементаў паслядоўнасці.
знаходзіцца бясконца
многа элементаў паслядоўнасці.
2.78.
Дадзены паслядоўнасці: ![]()
![]()
![]() Якая з гэтых
паслядоўнасцяў:
1) мае лімітавы пункт; 2) мае два лімітавыя пункты; 3) не
мае лімі-тавых пунктаў?
Якая з гэтых
паслядоўнасцяў:
1) мае лімітавы пункт; 2) мае два лімітавыя пункты; 3) не
мае лімі-тавых пунктаў?
2.79.
Колькі лімітавых пунктаў мае паслядоўнасць ![]() ? Знайдзіце
адпаведныя падпаслядоўнасці.
? Знайдзіце
адпаведныя падпаслядоўнасці.
2.80. Дакажыце, што збежная паслядоўнасць мае толькі адзін лімітавы пункт. Ці будзе праўдзівым адваротнае сцверджанне?
2.81.
Карыстаючыся вынікамі задачы 2.80, дакажыце
разбежнасць пасля-доўнасці ![]()
2.82.
Няхай у паслядоўнасці ![]() будуць
збежнымі падпаслядоўнасці
будуць
збежнымі падпаслядоўнасці ![]() і
(
і
(![]() ). Ці заўсёды з
гэтага вынікае збежнасць самой паслядоўнасці ?
). Ці заўсёды з
гэтага вынікае збежнасць самой паслядоўнасці ?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.