§ 1. Собственные векторы линейного оператора
Ненулевой вектор ![]() линейного
пространства V над полем P называется собственным
вектором линейного оператора
линейного
пространства V над полем P называется собственным
вектором линейного оператора ![]() , если существует такое
число
, если существует такое
число ![]() P, что
P, что
![]() =
= ![]() . (1)
. (1)
Число ![]() из
равенства (1) называется собственным значением оператора f,
соответствующим собственному вектору
из
равенства (1) называется собственным значением оператора f,
соответствующим собственному вектору ![]() .
.
Другими словами, собственным вектором линейного
оператора ![]() является такой вектор
линейного пространства V, который коллинеарен своему образу при
операторе f.
является такой вектор
линейного пространства V, который коллинеарен своему образу при
операторе f.
Свойства собственных векторов.
1º. Каждому собственному вектору соответствует единственное собственное значение.
2º. Собственные векторы с различными собственными значениями линейно независимы.
3º. Множество ![]() всех собственных векторов
линейного оператора
всех собственных векторов
линейного оператора ![]() с одним и тем же
собственным значением
с одним и тем же
собственным значением ![]() вместе с нулевым
вектором является подпространством линейного пространства V. Это
подпространство называется собственным
подпространством оператора f.
вместе с нулевым
вектором является подпространством линейного пространства V. Это
подпространство называется собственным
подпространством оператора f.
Пусть пространство V конечномерное, т.е.
![]() . Если А – матрица
линейного оператора
. Если А – матрица
линейного оператора ![]() в некотором
базисе, Х – координатный столбец собственного вектора
в некотором
базисе, Х – координатный столбец собственного вектора ![]() в том же базисе, то
равенство (1) равносильно равенству
в том же базисе, то
равенство (1) равносильно равенству
![]() . (2)
. (2)
Пример 1. Показать,
что в случае невырожденности линейного оператора ![]() операторы
операторы
![]() и
и ![]() имеют одни и те же
собственные векторы, и найти связь между их соответствующими собственными значениями.
имеют одни и те же
собственные векторы, и найти связь между их соответствующими собственными значениями.
►Если оператор ![]() невырожденный,
то
невырожденный,
то ![]() , поэтому нуль не может быть
собственным значением невырожденного линейного оператора. Обозначим
, поэтому нуль не может быть
собственным значением невырожденного линейного оператора. Обозначим ![]() – тождественный оператор.
Если
– тождественный оператор.
Если ![]() – собственный вектор
оператора
– собственный вектор
оператора ![]() с собственным значением
с собственным значением ![]() , то
, то
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
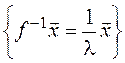 , т.е.
вектор
, т.е.
вектор ![]() удовлетворяет определению
собственного вектора оператора
удовлетворяет определению
собственного вектора оператора ![]() , причем
соответствующее собственное значение равно
, причем
соответствующее собственное значение равно ![]() .
Таким образом, взаимно обратные линейные операторы имеют одинаковые собственные
векторы, а их собственные значения – взаимно обратные числа.◄
.
Таким образом, взаимно обратные линейные операторы имеют одинаковые собственные
векторы, а их собственные значения – взаимно обратные числа.◄
Пример 2. Пусть
![]() и
и ![]() – собственные векторы
линейного оператора
– собственные векторы
линейного оператора ![]() с различными
собственными значениями,
с различными
собственными значениями, ![]() и
и ![]() – отличные от нуля числа. Доказать,
что вектор
– отличные от нуля числа. Доказать,
что вектор ![]() собственным не является.
собственным не является.
►Обозначим ![]() и
и ![]() – собственные значения
линейного оператора
– собственные значения
линейного оператора ![]() , соответствующие
собственным векторам
, соответствующие
собственным векторам ![]() и
и ![]() соответственно,
соответственно, ![]() . Предположим, что вектор
. Предположим, что вектор ![]() также является собственным
вектором оператора
также является собственным
вектором оператора ![]() , и пусть
, и пусть ![]() – его собственное значение.
Тогда
– его собственное значение.
Тогда
![]()
![]() [линейность
[линейность ![]() ]
] ![]()
![]()
![]()
![]() [векторы
[векторы
![]() и
и ![]() – собственные]
– собственные] ![]()
![]()
![]()
![]()
![]() .
.
В силу линейной независимости собственных векторов с
различными собственными значениями, из последнего равенства вытекает, что ![]() ,
, ![]() . Так как числа
. Так как числа ![]() и
и ![]() отличны от нуля, то
отличны от нуля, то ![]() ,
, ![]() , следовательно
, следовательно![]() , и мы пришли к противоречию.◄
, и мы пришли к противоречию.◄
Пример 3. Доказать, что а) собственные векторы линейного оператора, соответствующие собственному значению нуль, и только они лежат в ядре этого оператора;
б) собственные векторы, соответствующие ненулевым собственным значениям, лежат в образе этого оператора.
►Образомлинейного оператора ![]() называется
подмножество линейного пространства
называется
подмножество линейного пространства ![]()
![]() , а ядром – подмножество
линейного пространства
, а ядром – подмножество
линейного пространства ![]()
![]() . Известно, что
. Известно, что ![]() – подпространство пространства
– подпространство пространства
![]() , а
, а ![]() – подпространство пространства
– подпространство пространства
![]() .
.
а) Если ![]() , то
, то
{![]() –
собственный с собственным значением
–
собственный с собственным значением ![]() }
}![]()
![]() {
{![]() }
}![]() {
{![]() }.
}.
б) {![]() –
собственный с собственным значением
–
собственный с собственным значением ![]() }
} ![]() {
{![]() }
} ![]()
![]() {
{![]() }. Так как
}. Так как ![]() –
подпространство
–
подпространство ![]() , то оно замкнуто
относительно операции умножения на число, поэтому
, то оно замкнуто
относительно операции умножения на число, поэтому
{![]()
![]() }
}![]() {
{![]()
![]() }.◄
}.◄
Пример 4. В
некотором базисе трехмерного пространства ![]() линейный
оператор
линейный
оператор ![]() имеет
матрицу
имеет
матрицу 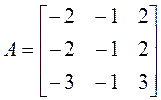 . Проверить, какие из
векторов
. Проверить, какие из
векторов ![]() ,
, ![]() и
и ![]() будут собственными
векторами этого оператора и указать их собственные значения.
будут собственными
векторами этого оператора и указать их собственные значения.
►Для каждого из заданных векторов проверяем условие (2):
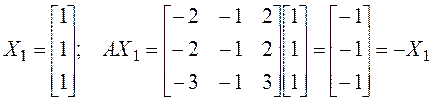 ,
, ![]() – собственный,
– собственный, ![]() ;
;
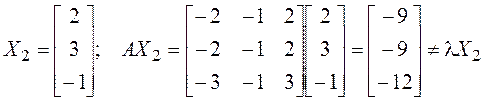 ,
, ![]() – не собственный;
– не собственный;
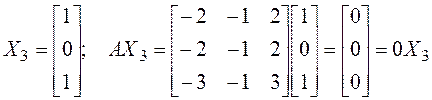 ,
, ![]() – собственный,
– собственный, ![]() .◄
.◄
Пример 5. В
пространстве ![]() задан линейный
оператор
задан линейный
оператор 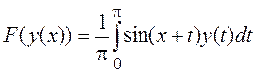 . Найти собственные функции
(собственные векторы) оператора
. Найти собственные функции
(собственные векторы) оператора ![]() и
соответствующие им собственные значения.
и
соответствующие им собственные значения.
►Для произвольной функции ![]()
![]()
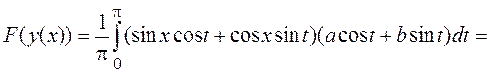
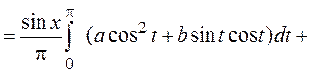
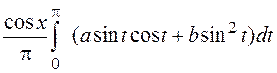 =
=
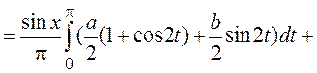
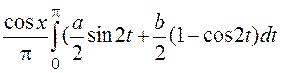 =
=![]() =
=![]() .
.
(при
вычислении интегралов использовалось свойство: интеграл от синуса или косинуса
по полному периоду равен нулю). Таким образом, все функции вида ![]() являются собственными
функциями заданного оператора с собственным значением, равным
являются собственными
функциями заданного оператора с собственным значением, равным ![]() .◄
.◄
Пример 6. Обозначим
![]() – линейное пространство
функций, определенных и бесконечное число раз непрерывно дифференцируемых на
всей числовой прямой,
– линейное пространство
функций, определенных и бесконечное число раз непрерывно дифференцируемых на
всей числовой прямой, ![]() – оператор
дифференцирования, ставящий в соответствие каждой функции ее производную (т.е.
– оператор
дифференцирования, ставящий в соответствие каждой функции ее производную (т.е. ![]() ),
), ![]() – тождественный оператор.
Показать, что функция
– тождественный оператор.
Показать, что функция ![]() является
собственной функцией как линейного оператора
является
собственной функцией как линейного оператора ![]() ,
так и линейного оператора
,
так и линейного оператора ![]() , тогда
как
, тогда
как ![]() является собственной функцией
линейного оператора
является собственной функцией
линейного оператора ![]() , но не будет
собственной функцией оператора
, но не будет
собственной функцией оператора ![]() .
.
►Проводим проверку непосредственно по определению:
![]() ,
, ![]() ;
;
![]() ,
, ![]() ;
;
![]() ;
;
![]() ,
, ![]() .◄
.◄
Правило нахождения
собственных векторов. Обозначим А матрицу линейного оператора
![]() в некотором базисе
конечномерного линейного пространства
в некотором базисе
конечномерного линейного пространства ![]() над
полем
над
полем ![]() , а Х – координатный столбец вектора
, а Х – координатный столбец вектора ![]() в том же базисе.
в том же базисе.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.