Собственные векторы линейного оператора. Свойства собственных векторов, страница 3

Разделим последнюю строку матрицы (5) на четыре с целью уменьшения чисел, что не изменит решения системы, и найдем одно из решений, используя алгебраические дополнения к элементам первой строки:

, , , , .

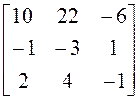б) Поступаем, как и в предыдущем случае (алгебраические дополнения опять к первой строке):

, ;

, , , .◄

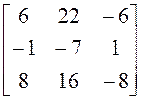
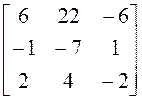Пример 8. Найти собственные векторы линейного оператора , который в некотором базисе действительного линейного пространства V₃ имеет матрицу

.

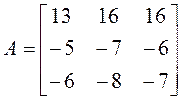►Находим характеристический многочлен матрицы А:

  

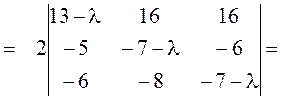
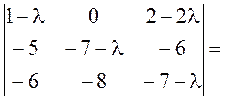
– 2

=.

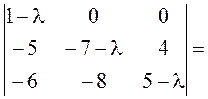
Этот многочлен имеет следующие корни:  кратности два и . Оба они действительны, поэтому оба являются собственными значениями. Для каждого из собственных значений  находим собственные векторы, решая однородную систему с матрицей : а) , .

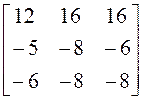Ранг матрицы равен двум, один из собственных векторов можно найти, используя алгебраические дополнения, например, к элементам первой строки: ,  , . б) , .   

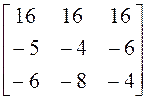Ранг матрицы опять равен двум, значит, опять один из собственных векторов можно найти, используя алгебраические дополнения, например, к элементам первой строки: ,  , .◄

Пример 9. Найти собственные векторы линейного оператора , который в некотором базисе действительного линейного пространства V₃ имеет матрицу

.

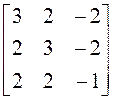►Характеристический многочлен:

                      +

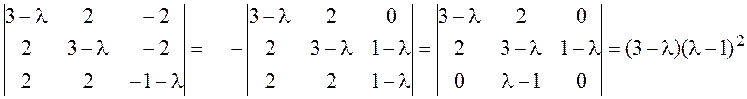Этот многочлен имеет корни  кратности 2 и , которые будут и собственными значениями. Находим собственные векторы: а) , .

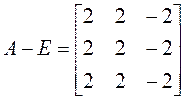Метод алгебраических дополнений в данном случае не дает желаемого результата: упорядоченный набор из алгебраических дополнений к элементам любой строчки будет тривиальным, т.к. все они пропорциональны. Решаем систему обычным образом: из единственного ее независимого уравнения  получаем . Полагая , получаем , , где, , . б) , , , , .◄

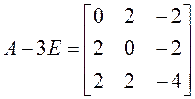Обратите внимание на следующий факт: если в примере 8 двукратному собственному значению соответствует одномерное подпространство, то в примере 9 – двумерное.

◄

Пример 10. Найти собственные векторы линейного оператора , который в некотором базисе действительного линейного пространства V₃ имеет матрицу

.

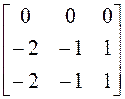►Характеристический многочлен:

.

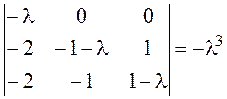Этот многочлен имеет только один корень  кратности 3, который будет и собственным значением. Находим собственные векторы:

, .

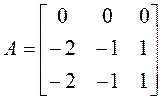И опять нельзя использовать метод алгебраических дополнений. Решая систему обычным образом, получаем . Положим , тогда , , где, , . ◄

Пример 11. Найти собственные векторы линейного оператора , который в некотором базисе комплексного линейного пространства V₃ имеет матрицу

.

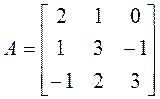►Составляем характеристический многочлен:

.

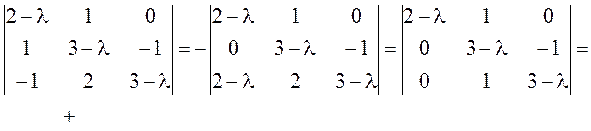
Характеристическое уравнение оператора  выглядит так:

, а характеристическими числами будут . Так как линейный оператор действует в комплексном пространстве, т о все его характеристические числа являются и собственными значениями. Найдем собственные векторы.

а) , .

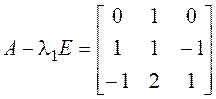Однородная система с такой матрицей решается устно: . Значит, собственные векторы с этим собственным значением выглядят так: , , . б) , .     

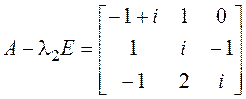Так как все собственные значения однократны, то и все собственные подпространства  одномерны, поэтому для каждого из них достаточно найти по одному собственному вектору, что можно сделать при помощи алгебраических дополнений. Выберем, например, алгебраические дополнения к элементам первой строки матрицы: , , .

в) , .      

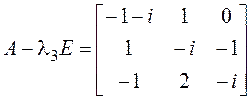Мы получили матрицу, комплексно-сопряженную предыдущей. Значит, и решения систем с этими матрицами – тоже комплексно-сопряженные, и поэтому ◄

Пример 12. В пространстве  многочленов степени не выше двух задан линейный оператор 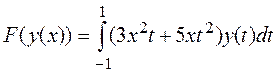. Найти собственные функции (собственные векторы) оператора  и соответствующие им собственные значения.