Собственные векторы линейного оператора. Свойства собственных векторов, страница 2

Характеристическим многочленом линейного оператора  и его матрицы А называется многочлен . Уравнение

,                                            (3)

называется характеристическим уравнением оператора  и его матрицы, а корни этого уравнения – их характеристическими числами. Справедливы следующие утверждения:

а) собственными значениями линейного оператора являются его характеристические числа, принадлежащие полю , и только они;

б) для каждого собственного значения  ненулевые столбцы-решения однородной системы линейных уравнений

                                              (4)

являются координатными столбцами собственных векторов оператора , соответствующих собственному значению ;

в) .

Из вышесказанного вытекает следующий алгоритм нахождения собственных векторов.

1. Составляем характеристическое уравнение матрицы  и находим его корни . Те из них, которые принадлежат полю , будут собственными значениями.

2. Для каждого из найденных собственных значений  находим соответствующие ему собственные векторы, решая однородную систему линейных уравнений (4) при условии, что .

Замечания. 1. Для любой вырожденной квадратной однородной системы линейных уравнений  () упорядоченный набор, состоящий из алгебраических дополнений к элементам какой-либо строки ее матрицы, является решением этой системы (доказательство см., например, в []).

2. Характеристическое уравнение линейного оператора в -мерном линейном пространстве имеет -тую степень, и в общем случае для его решения нет никаких формул. Поэтому характеристический многочлен целесообразно разложить на множители еще на стадии его вычисления. Например, при вычислении определителя третьего порядка следует обращать внимание на элементы, отмеченные в (4.5) одинаковым образом:

                                         .                         

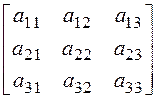
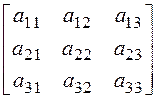Применяя элементарные преобразования в первом случае к столбцам матрицы, а во втором – к ее строкам, добиваемся, чтобы один из двух отмеченных одинаковым образом элементов обратился в нуль. При этом из предложенных шести преобразований следует выбирать такое, после которого отличные от нуля элементы в преобразованной строке или столбце имеют общий множитель.

Пример 7. Найти собственные векторы линейного оператора , который в некотором базисе действительного линейного пространства V₃ имеет матрицу

.

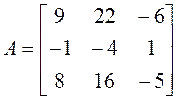►Находим характеристический многочлен матрицы А, отмечая стрелками применяемые элементарные преобразования:

  –

+

=.

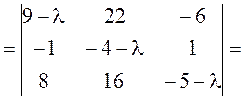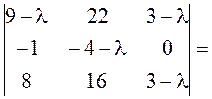
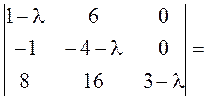
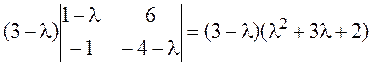Этот многочлен имеет корни . Все они действительны, поэтому все являются собственными значениями. Для каждого из собственных значений  находим собственные векторы, решая однородную систему с матрицей : а) , 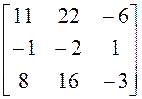. Решим систему методом исключения неизвестных, для чего упростим ее матрицу, применяя элементарные преобразования только к строкам. В результате этих действий получаем матрицу системы, равносильной исходной, поэтому между матрицами будем ставить знак равносильности :

          .

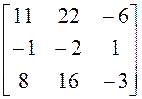
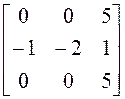
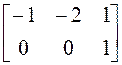
Базисными неизвестными последней системы можно выбрать первое и третье, второе будет свободным. Тогда общее решение примет вид: . Если положить , то получаем множество всех собственных векторов с собственным значением : , или , где , . б) , .                                              (5)

Метод исключения неизвестных для решения системы в данном случае хорош тем, что позволяет быстро обнаружить ошибку в случае неверного нахождения собственного значения: если  найдено неверно, то  и система  будет иметь единственное тривиальное решение. Если же вы уверены в правильности своих вычислений, то в случае однократных собственных значений решать систему, конечно же, удобнее на основании замечания 1. В этом случае , так как трем он не может равняться в силу выбора  (определитель равен нулю), а единице – из-за того, что нет пропорциональных строк. Поэтому , значит, все собственные векторы с этим собственным значением коллинеарны между собой. Если мы найдем один из них, то для получения всех остальных останется умножить его на произвольное ненулевое число.