►1-й способ.
![]()
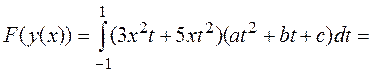
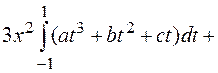
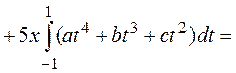
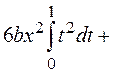
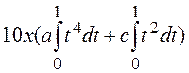 =
=![]()
![]()
(при
вычислении интегралов использовались следующие их свойства: интеграл от
нечетной функции по симметричному промежутку равен нулю; интеграл от четной функции
по симметричному промежутку равен удвоенному интегралу от той же функции по
правой половине промежутка). Если ![]() – собственная функция, то
для некоторого
– собственная функция, то
для некоторого ![]()
![]() , т.е.,
, т.е.,
![]()
![]() =
=![]() (6)
(6)
Равенство
(6) следует рассматривать как равенство функций, значит, оно справедливо при
любом ![]() . Это возможно в том и только
в том случае, когда коэффициенты при соответствующих степенях переменной
. Это возможно в том и только
в том случае, когда коэффициенты при соответствующих степенях переменной ![]() совпадают. Получаем систему
уравнений
совпадают. Получаем систему
уравнений
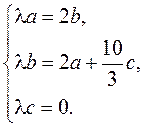
Возможны два случая:
а) ![]() . Тогда
. Тогда ![]() ,
, ![]() , значит,
, значит,
![]() . Одной из таких функций
будет
. Одной из таких функций
будет ![]() , а все остальные ей пропорциональны.
, а все остальные ей пропорциональны.
б) ![]() . Тогда
. Тогда 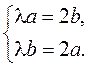 Если
Если ![]() , то и
, то и ![]() , и наоборот. В этом случае
, и наоборот. В этом случае ![]() , что противоречит
определению собственного вектора. Если же
, что противоречит
определению собственного вектора. Если же ![]() ,
то, разделив первое уравнение на второе, находим
,
то, разделив первое уравнение на второе, находим 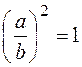 , т.е.,
, т.е., ![]() . При
. При ![]()
![]() ,
,
![]() ; при
; при ![]()
![]() ,
,
![]() (все остальные ей пропорциональны).
(все остальные ей пропорциональны).
2-й способ.
Составим матрицу линейного оператора ![]() в базисе
в базисе
![]() .
Для этого, как обычно, найдем образы этих функций:
.
Для этого, как обычно, найдем образы этих функций:
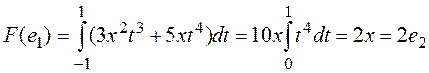 ,
, 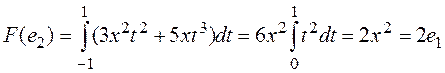 ,
,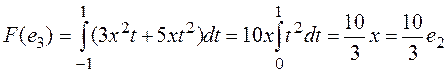 .
.
Матрица
оператора ![]() в выбранном базисе имеет
вид
в выбранном базисе имеет
вид
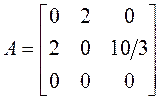 .
.
Тогда
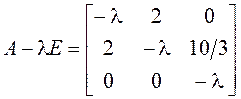 ,
, ![]() ,
, ![]() .
.
а) ![]() ,
, 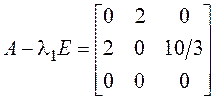 ,
, ![]() ,
, ![]()
(все остальные ей пропорциональны);
б) ![]() ,
, 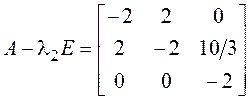 ,
, ![]() ,
, ![]()
(все остальные ей пропорциональны);
в) ![]() ,
, 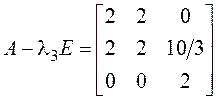 ,
, ![]() ,
, ![]()
(все остальные ей пропорциональны).◄
Пример
13. В комплексном линейном пространстве ![]() комплексных
квадратных матриц второго порядка рассматривается следующий линейный оператор:
комплексных
квадратных матриц второго порядка рассматривается следующий линейный оператор: ![]() :
: ![]() . Найдите собственные значения
и максимальную линейно независимую систему собственных векторов этого оператора,
если
. Найдите собственные значения
и максимальную линейно независимую систему собственных векторов этого оператора,
если 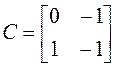 . Если полученная система
является базисом, запишите в нем матрицу оператора
. Если полученная система
является базисом, запишите в нем матрицу оператора ![]() .
.
►Составим матрицу линейного оператора ![]() в базисе
в базисе 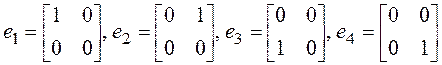 , для
чего найдем образы этих матриц:
, для
чего найдем образы этих матриц:
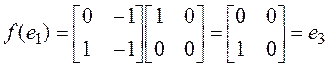 ,
, 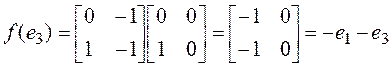 ,
, 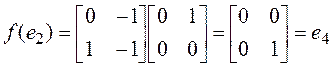 ,
,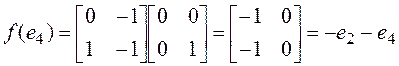
Матрица
оператора ![]() в выбранном базисе имеет
вид
в выбранном базисе имеет
вид
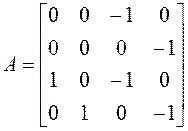 .
.
Определитель
матрицы ![]() вычислим по теореме
Лапласа, выделяя первую и третью строчки. Единственный отличный от нуля минор
второго порядка в этих строчках расположен в первом и третьем столбцах. Тогда
вычислим по теореме
Лапласа, выделяя первую и третью строчки. Единственный отличный от нуля минор
второго порядка в этих строчках расположен в первом и третьем столбцах. Тогда
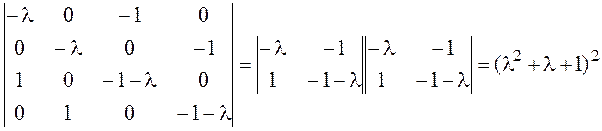 .
.
Этот многочлен имеет два различных комплексных корня ![]()
![]() и
и
![]() , каждый из которых имеет
кратность, равную двум.
, каждый из которых имеет
кратность, равную двум.
а) ![]() ,
, ![]() =
=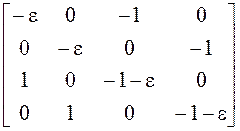 .
.
Система
с такой матрицей имеет два линейно независимых решения: ![]() и
и ![]() , значит, этому собственному значению соответствуют две
матрицы:
, значит, этому собственному значению соответствуют две
матрицы: 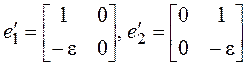 .
.
б) ![]() ,
, 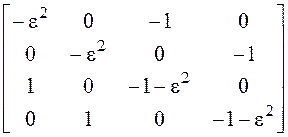
![]()
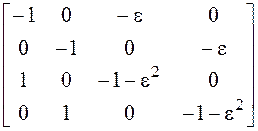 .
.
Система
с этой матрицей также имеет два линейно независимых решения: ![]() и
и ![]() , этому собственному значению соответствуют матрицы:
, этому собственному значению соответствуют матрицы: 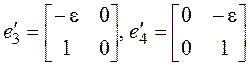 .
.
Итак, в четырехмерном пространстве мы нашли четыре
линейно независимых собственных вектора, значит, они образуют базис. Матрица
оператора ![]() в базисе
в базисе ![]() выглядит так:
выглядит так:
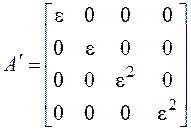 .◄
.◄
Задачи
1.
В трехмерном пространстве ![]() свободных векторов
задан ортонормированный базис
свободных векторов
задан ортонормированный базис ![]() . Найдите собственные
векторы и их собственные значения для следующих линейных операторов
. Найдите собственные
векторы и их собственные значения для следующих линейных операторов ![]() : а)
: а) ![]() – поворот вектора вокруг
оси
– поворот вектора вокруг
оси ![]() на угол
на угол ![]() ;
;
б)
![]() – проектирование на
плоскость
– проектирование на
плоскость ![]() ;
;
в)
![]() – проектирование на ось;
– проектирование на ось;
г)
![]() – симметрия относительно
плоскости
– симметрия относительно
плоскости ![]() ; д)
; д)
![]() – симметрия относительно
оси
– симметрия относительно
оси ![]() ;
;
е)
![]() – симметрия относительно
начала координат.
– симметрия относительно
начала координат.
2.
Пусть ![]() – ненулевой вектор
пространства свободных векторов
– ненулевой вектор
пространства свободных векторов ![]() . Найдите собственные
значения и собственные векторы следующих линейных операторов
. Найдите собственные
значения и собственные векторы следующих линейных операторов ![]() : а)
: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3.
Линейный оператор ![]() в некотором базисе
пространства
в некотором базисе
пространства ![]() задан матрицей
задан матрицей ![]() . Проверьте, какой из
векторов
. Проверьте, какой из
векторов ![]() или
или ![]() является собственным
вектором этого оператора и найдите его собственное значение, если:
является собственным
вектором этого оператора и найдите его собственное значение, если:
а) 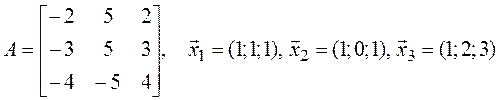 ; б)
; б)
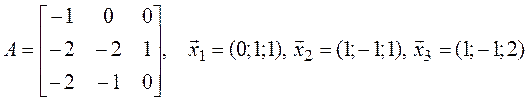 ;
;
в)
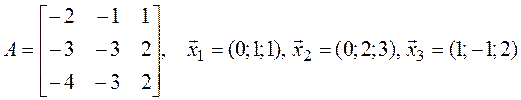 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.