4.
Обозначим ![]() – линейное пространство
функций, определенных и бесконечное число раз непрерывно дифференцируемых на
всей числовой прямой,
– линейное пространство
функций, определенных и бесконечное число раз непрерывно дифференцируемых на
всей числовой прямой, ![]() – оператор
дифференцирования, ставящий в соответствие каждой функции ее производную (т.е.
– оператор
дифференцирования, ставящий в соответствие каждой функции ее производную (т.е. ![]() ),
), ![]() – тождественный оператор.
Покажите, что функция
– тождественный оператор.
Покажите, что функция ![]() является
собственной функцией линейного оператора
является
собственной функцией линейного оператора ![]() и
найдите ее собственное значение
и
найдите ее собственное значение ![]() в каждом
из следующих случаев:
в каждом
из следующих случаев:
а) ![]() (с – константа); б)
(с – константа); б)
![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() .
.
5.
В каждом из
перечисленных случаев проверьте, являются ли собственными функциями линейного
оператора ![]() функции
функции ![]() и
и ![]() , а также для собственных
функций найдите их собственные значения, если: а)
, а также для собственных
функций найдите их собственные значения, если: а)
![]() ;
б)
;
б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
6.
Покажите, что собственными
функциями линейного оператора 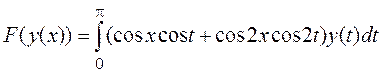 пространства
пространства
![]() в себя являются функции
в себя являются функции ![]() и
и ![]() , а также укажите их собственные
значения.
, а также укажите их собственные
значения.
7.
В пространстве ![]() многочленов степени не выше
двух задан линейный оператор
многочленов степени не выше
двух задан линейный оператор 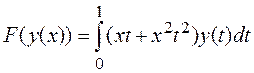 .
Покажите, что функция
.
Покажите, что функция ![]() является
собственной функцией этого оператора и найдите ее собственной значение.
является
собственной функцией этого оператора и найдите ее собственной значение.
8.
Покажите, что при умножении
линейного оператора на ненулевое число ![]() множество
собственных векторов не меняется. Изменяются ли при этом собственные значения?
множество
собственных векторов не меняется. Изменяются ли при этом собственные значения?
9.
Покажите, что собственный
вектор линейного оператора ![]() является
собственным вектором и для оператора
является
собственным вектором и для оператора ![]() . Верно
ли обратное утверждение?
. Верно
ли обратное утверждение?
10.
Покажите, что для любого
многочлена ![]() собственный вектор
линейного оператора
собственный вектор
линейного оператора ![]() является
собственным вектором и для оператора
является
собственным вектором и для оператора ![]() , и
найдите связь между соответствующими собственными значениями.
, и
найдите связь между соответствующими собственными значениями.
11.
Докажите, что все ненулевые
векторы линейного пространства V над полем P тогда
и только тогда являются собственными векторами оператора ![]() , когда
, когда ![]() , где
, где ![]() – тождественный оператор.
– тождественный оператор.
12.
Линейные операторы ![]() и
и ![]() называются перестановочными,
если
называются перестановочными,
если ![]() . Докажите, что если
линейный оператор
. Докажите, что если
линейный оператор ![]() имеет
имеет ![]() различных собственных
значений, то любой линейный оператор
различных собственных
значений, то любой линейный оператор ![]() ,
перестановочный с
,
перестановочный с ![]() , имеет те же
собственные векторы, что и
, имеет те же
собственные векторы, что и ![]() .
.
13. Докажите, что любые два перестановочных линейных оператора конечномерного комплексного линейного пространства в себя имеют общий собственный вектор.
14.
Линейный оператор ![]() линейного пространства V3 над полем Р в себя в некотором базисе
имеет матрицу А. Найдите собственные значения и собственные векторы этого
оператора в случае, когда: а)
P = R, б) P = C.
линейного пространства V3 над полем Р в себя в некотором базисе
имеет матрицу А. Найдите собственные значения и собственные векторы этого
оператора в случае, когда: а)
P = R, б) P = C.
1) 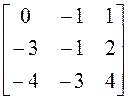 ; 2)
; 2)
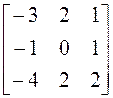 ;
3)
;
3) 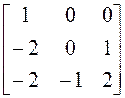 ; 4)
; 4) 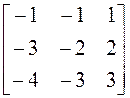 ;
;
5) 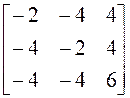 ; 6)
; 6)
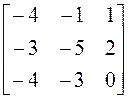 ; 7)
; 7) 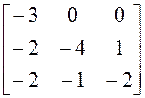 ; 8)
; 8) 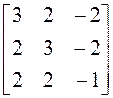 ;
;
9) 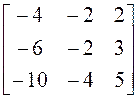 ; 10)
; 10) 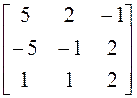 ; 11)
; 11) 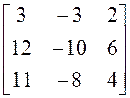 ; 12)
; 12) 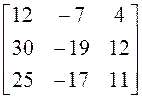 ;
;
13)
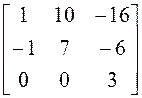 ; 14)
; 14) 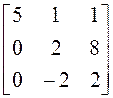 ; 15)
; 15) 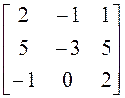 ; 16)
; 16) 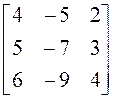 ;
;
17)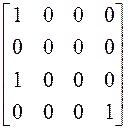 ;18)
;18)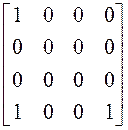 ; 19)
; 19) 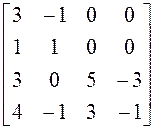 ;20)
;20) 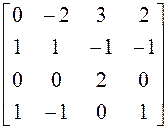
15. Докажите, что корни характеристического многочлена треугольной (в частности, диагональной) матрицы совпадают с ее диагональными элементами.
16. Докажите, что характеристический многочлен блочно-треугольной (блочно-диагональной) матрицы равен произведению характеристических многочленов ее диагональных блоков.
17.
В линейном пространстве ![]() задан линейный оператор
задан линейный оператор 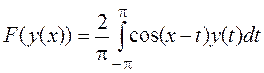 . Найдите собственные
значения и собственные функции этого оператора.
. Найдите собственные
значения и собственные функции этого оператора.
18.
В линейном пространстве многочленов
степени не выше двух задан линейный оператор ![]() .
Найдите собственные значения и собственные функции этого линейного оператора,
если:
.
Найдите собственные значения и собственные функции этого линейного оператора,
если:
а)
![]() ; б)
; б)![]() в)
в) ![]() ;
;
г)
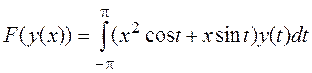 ; д)
; д) 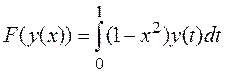 .
.
19.
В пространстве ![]() действительных квадратных
матриц второго порядка рассматривается линейный оператор транспонирования:
действительных квадратных
матриц второго порядка рассматривается линейный оператор транспонирования: ![]() :
: ![]() . Найдите собственные значения
и собственные векторы этого оператора.
. Найдите собственные значения
и собственные векторы этого оператора.
20.
В пространстве ![]() действительных квадратных
матриц второго порядка рассматривается следующий линейный оператор:
действительных квадратных
матриц второго порядка рассматривается следующий линейный оператор: ![]() :
: ![]() . Найдите собственные
значения и собственные векторы этого оператора, если: а)
. Найдите собственные
значения и собственные векторы этого оператора, если: а) 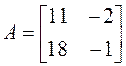 ; б)
; б) 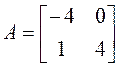 .
.
Составила доцент Березкина Л.Л.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.