ТЕСТ ПО СИСТЕМАМ ЛИНЕЙНЫХ УРАВНЕНИЙ (4-е занятие)
1.
Пусть
![]() ,
, ![]() и
и ![]() -
невырожденные квадратные матрицы
-
невырожденные квадратные матрицы ![]() -го порядка.
Решением матричного уравнения
-го порядка.
Решением матричного уравнения ![]() является
матрица: а)
является
матрица: а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д) другой
ответ.
; д) другой
ответ.
2.
Задана
система линейных уравнений 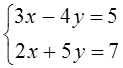 . Для этой
системы:
. Для этой
системы:
а) 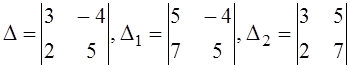 ; б)
; б) 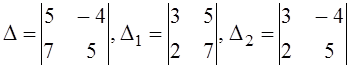 ; в)
; в)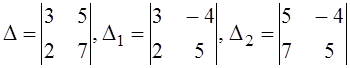 ; г)
; г) 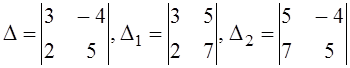 ; д)другой
ответ.
; д)другой
ответ.
3. Если ранг матрицы равен 5, то следующие утверждения верны:
а) все ее миноры 5-го порядка равны нулю; б) существует минор 5-го порядка, отличный от нуля; в) все ее миноры 5-го порядка отличны от нуля; г) все ее миноры 4-го порядка равны нулю; д) существует минор 4-го порядка, отличный от нуля; е) все ее миноры 4-го порядка отличны от нуля; ж) все ее миноры 6-го порядка равны нулю; з) существует минор 6-го порядка, отличный от нуля; е) все ее миноры 6-го порядка отличны от нуля.
4.
Если
матрицу ![]() умножить на
3, то ее ранг: а)
умножится на 3; б) умножится на
умножить на
3, то ее ранг: а)
умножится на 3; б) умножится на ![]() ; в) не
изменится; г) другой ответ.
; в) не
изменится; г) другой ответ.
5.
Если
в матрице ![]() две строки
поменять местами, то ее ранг: а)
поменяет знак; б) умножится на 2; в) не
изменится; г) другой ответ.
две строки
поменять местами, то ее ранг: а)
поменяет знак; б) умножится на 2; в) не
изменится; г) другой ответ.
6.
Если
в матрице ![]() один столбец
умножить на 2, а второй на 8, то ее ранг: а)
умножится на 16; б) умножится на 2; в) не изменится; г) другой ответ.
один столбец
умножить на 2, а второй на 8, то ее ранг: а)
умножится на 16; б) умножится на 2; в) не изменится; г) другой ответ.
7. Если в матрице вычеркнуть одну строку, то ее ранг:
а) может повыситься; б) может понизиться; в) не изменится; г) другой ответ.
8. Если в матрице вычеркнуть столбец, состоящий из нулей, то ее ранг:
а) может повыситься; б) может понизиться; в) не изменится; г) другой ответ.
9.
Если
строки матицы ![]() линейно
независимы, то: а)
линейно
независимы, то: а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г) другой
ответ.
; г) другой
ответ.
10.
Если
столбцы матицы ![]() линейно
зависимы, то: а)
линейно
зависимы, то: а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г) другой
ответ.
; г) другой
ответ.
11.
Дана
матрица ![]() . Если
. Если ![]() , то: а)
строки матицы
, то: а)
строки матицы ![]() линейно
независимы; б) строки матицы
линейно
независимы; б) строки матицы ![]() линейно
зависимы; в) такого не может быть; г) другой ответ.
линейно
зависимы; в) такого не может быть; г) другой ответ.
12.
Дана
матрица ![]() . Если
. Если ![]() , то: а)
строки матицы
, то: а)
строки матицы ![]() линейно
независимы; б) строки матицы
линейно
независимы; б) строки матицы ![]() линейно
зависимы; в) такого не может быть; г) другой ответ.
линейно
зависимы; в) такого не может быть; г) другой ответ.
13.
Дана
матрица ![]() . Если
. Если ![]() , то: а)
столбцы матицы
, то: а)
столбцы матицы ![]() линейно
независимы; б) столбцы матицы
линейно
независимы; б) столбцы матицы ![]() линейно
зависимы; в) такого не может быть; г) другой ответ.
линейно
зависимы; в) такого не может быть; г) другой ответ.
14.
Дана
матрица ![]() . Если
. Если ![]() , то: а)
столбцы матицы
, то: а)
столбцы матицы ![]() линейно
независимы; б) столбцы матицы
линейно
независимы; б) столбцы матицы ![]() линейно
зависимы; в) такого не может быть; г) другой ответ.
линейно
зависимы; в) такого не может быть; г) другой ответ.
15.
Задана
система линейных уравнений ![]() с
с ![]() неизвестными.
Если
неизвестными.
Если ![]() , то эта
система: а)
имеет решение; б) имеет единственное решение; в) не имеет решения; г) имеет
бесчисленное множество решений; д) такого не может быть; е) другой ответ.
, то эта
система: а)
имеет решение; б) имеет единственное решение; в) не имеет решения; г) имеет
бесчисленное множество решений; д) такого не может быть; е) другой ответ.
16.
Задана
система линейных уравнений ![]() с
с ![]() неизвестными.
Если
неизвестными.
Если ![]() , то эта
система: а)
имеет решение; б) имеет единственное решение; в) не имеет решения; г) имеет
бесчисленное множество решений; д) такого не может быть; е) другой ответ.
, то эта
система: а)
имеет решение; б) имеет единственное решение; в) не имеет решения; г) имеет
бесчисленное множество решений; д) такого не может быть; е) другой ответ.
17.
Задана
система линейных уравнений ![]() с
с ![]() неизвестными.
Если
неизвестными.
Если ![]() , то эта
система: а)
имеет решение; б) имеет единственное решение; в) не имеет решения; г) имеет
бесчисленное множество решений; д) такого не может быть; е) другой ответ.
, то эта
система: а)
имеет решение; б) имеет единственное решение; в) не имеет решения; г) имеет
бесчисленное множество решений; д) такого не может быть; е) другой ответ.
18.
Задана
система линейных уравнений ![]() с
с ![]() неизвестными.
Если
неизвестными.
Если ![]() , то эта
система: а)
имеет решение; б) имеет единственное решение; в) не имеет решения; г) имеет
бесчисленное множество решений; д) такого не может быть; е) другой ответ.
, то эта
система: а)
имеет решение; б) имеет единственное решение; в) не имеет решения; г) имеет
бесчисленное множество решений; д) такого не может быть; е) другой ответ.
19. Известно,
что система линейных уравнений с матрицей ![]() имеет
единственное решение. Тогда: а)
такого не может быть; б)
имеет
единственное решение. Тогда: а)
такого не может быть; б) ![]() ; в)
; в) ![]() ; г)
; г)![]() ; д)
; д) ![]() .
.
20. При каких действиях над расширенной матрицей системы линейных уравнений получается матрица системы, равносильной исходной: а) умножение строки на 0; б) умножение строки на число, отличное от нуля; в)прибавление к какой-либо строке другой строки, умноженной на число; г) перестановка строк; д) умножение столбца на 0; е) умножение столбца на число, отличное от нуля; ж) прибавление к какому -либо столбцу другого столбца, умноженного на число; з) перестановка столбцов.
21. Количество решений в фундаментальной системе решений однородной системы линейных уравнений равно: а) числу неизвестных; б) числу базисных неизвестных; в) числу свободных неизвестных; г) другой ответ.
22.
Известно, что ![]() . Какой из ее
перечисленных миноров может служить в качестве базисного:
. Какой из ее
перечисленных миноров может служить в качестве базисного:
а)
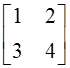 ; б)
; б) 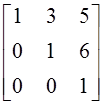 ; в)
; в) 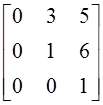 ; г)
; г)  ; д) другой
ответ.
; д) другой
ответ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.