§ 4. Жорданова нормальная форма матрицы
Жордановой клеткой ![]() -го порядка
называется матрица
-го порядка
называется матрица ![]() -го порядка
-го порядка
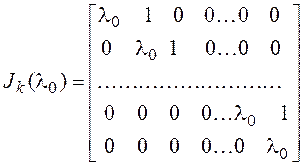 или
или 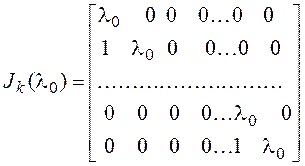 .
.
Ужордановой клетки все диагональные элементы одинаковые, диагональ, параллельная главной и расположенная над ней или под ней, состоит из единиц, а все остальные элементы равны нулю.
Характеристический многочлен жордановой клетки ![]() выглядит так:
выглядит так: ![]() . Таким образом, жорданова
клетка
. Таким образом, жорданова
клетка ![]() имеет единственное характеристическое
число
имеет единственное характеристическое
число ![]() , причем его кратность равна
порядку этой клетки. В дальнейшем мы будем использовать жордановы клетки только
первого вида. Примеры жордановых клеток:
, причем его кратность равна
порядку этой клетки. В дальнейшем мы будем использовать жордановы клетки только
первого вида. Примеры жордановых клеток:
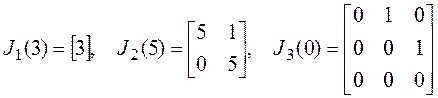 .
.
Пусть матрица линейного оператора ![]() в некотором базисе
в некотором базисе
![]()
пространства
![]() совпадает с жордановой клеткой
совпадает с жордановой клеткой ![]() первого вида. Тогда:
первого вида. Тогда:
![]() .
.
Отсюда видно, что первый вектор этого
базиса – собственный с собственным значением ![]() ,
а остальные – присоединенные к нему.
,
а остальные – присоединенные к нему.
Жордановой
матрицей называется блочно
диагональная матрица ![]() , диагональными
блоками которой являются жордановы клетки:
, диагональными
блоками которой являются жордановы клетки: ![]() .
В этой матрице числа
.
В этой матрице числа ![]() , также как и числа
, также как и числа ![]() могут совпадать или быть
различными. В частности, диагональная матрица является жордановой, все ее
клетки имеют первый порядок.
могут совпадать или быть
различными. В частности, диагональная матрица является жордановой, все ее
клетки имеют первый порядок.
Для любой комплексной квадратной
матрицы А существует невырожденная матрица Т такая, что матрица ![]() – жорданова.
– жорданова.
Матрица ![]() называется жордановой
нормальной формой матрицы А. Жорданова нормальная форма
матрицы определяется однозначно с точностью до порядка следования клеток.
Жорданова нормальная форма действительной матрицы А может оказаться
матрицей комплексной. Она будет действительной в том и только в том случае,
когда матрица имеет только действительные характеристические числа.
называется жордановой
нормальной формой матрицы А. Жорданова нормальная форма
матрицы определяется однозначно с точностью до порядка следования клеток.
Жорданова нормальная форма действительной матрицы А может оказаться
матрицей комплексной. Она будет действительной в том и только в том случае,
когда матрица имеет только действительные характеристические числа.
Свойства жордановой матрицы. 1. Характеристический многочлен жордановой матрицы равен произведению характеристических многочленов составляющих ее жордановых клеток.
2. Диагональными элементами клеток, составляющих жорданову нормальную форму матрицы А, являются ее характеристические числа или собственные значения, что для комплексной матрицы одно и то же.
3. Сумма порядков всех клеток, соответствующих одному и тому же собственному значению, равна кратности этого собственного значения.
4. Число клеток, соответствующих одному и тому же собственному значению, равно количеству линейно независимых собственных векторов с этим собственным значением.
5. Число клеток порядка выше ![]() ,
соответствующих данному собственному значению, равно количеству линейно
независимых собственных векторов с этим собственным значением, имеющих
,
соответствующих данному собственному значению, равно количеству линейно
независимых собственных векторов с этим собственным значением, имеющих ![]() -е присоединенные векторы.
-е присоединенные векторы.
Пример 1. Записать жорданову
нормальную форму матрицы пятого порядка в том случае, когда она имеет одно собственное
значение ![]() кратности пять.
кратности пять.
►Возможны следующие принципиально различные случаи:
1) ![]() . Это значит, линейный оператор
имеет пять линейно независимых векторов, следовательно, жорданова форма имеет
пять клеток. Так как сумма их порядков равна пяти, то все они имеют первый
порядок, значит,
. Это значит, линейный оператор
имеет пять линейно независимых векторов, следовательно, жорданова форма имеет
пять клеток. Так как сумма их порядков равна пяти, то все они имеют первый
порядок, значит,
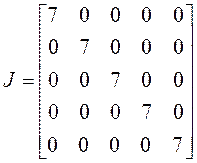 ;
;
2) ![]() . Линейный оператор имеет
четыре линейно независимых вектора, жорданова форма имеет четыре клетки, сумма
их порядков равна пяти. Число пять можно разбить на четыре слагаемых только
одним способом: одна двойка и три единицы. Соответственно жорданова форма имеет
одну клетку второго порядка и три клетки первого порядка:
. Линейный оператор имеет
четыре линейно независимых вектора, жорданова форма имеет четыре клетки, сумма
их порядков равна пяти. Число пять можно разбить на четыре слагаемых только
одним способом: одна двойка и три единицы. Соответственно жорданова форма имеет
одну клетку второго порядка и три клетки первого порядка:
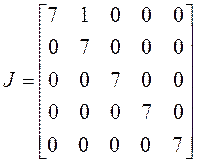 ;
;
3) ![]() . Линейный оператор имеет три
линейно независимых вектора, жорданова форма имеет три клетки. На три слагаемых
число пять можно разбить двумя способами: а) тройка и две единицы, б) две
двойки и единица. Чтобы эти случаи различить, надо знать количество линейно
независимых собственных векторов, имеющих присоединенные. Если такой вектор
один, имеем случай а), если два – то б):
. Линейный оператор имеет три
линейно независимых вектора, жорданова форма имеет три клетки. На три слагаемых
число пять можно разбить двумя способами: а) тройка и две единицы, б) две
двойки и единица. Чтобы эти случаи различить, надо знать количество линейно
независимых собственных векторов, имеющих присоединенные. Если такой вектор
один, имеем случай а), если два – то б):
а) 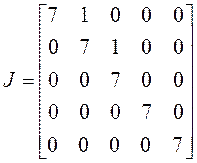 ,
б)
,
б) 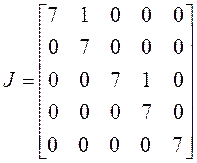 ;
;
4) ![]() . Жорданова форма имеет две
клетки. Опять может быть два случая: а) по одной клетке четвертого и первого
порядка, б) по одной клетке третьего и второго порядка. Если только один из
собственных векторов имеет присоединенные, имеем случай а), если оба – то б):
. Жорданова форма имеет две
клетки. Опять может быть два случая: а) по одной клетке четвертого и первого
порядка, б) по одной клетке третьего и второго порядка. Если только один из
собственных векторов имеет присоединенные, имеем случай а), если оба – то б):
а) 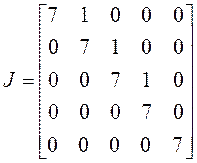 ,
б)
,
б) 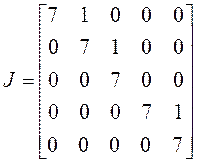 ;
;
5) ![]() . Жорданова форма имеет только
одну клетку пятого порядка:
. Жорданова форма имеет только
одну клетку пятого порядка:
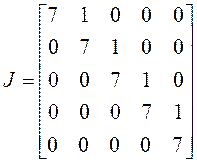 .◄
.◄
Для определения
числа ![]() клеток
клеток ![]() го порядка, соответствующих
собственному значению
го порядка, соответствующих
собственному значению ![]() в жордановой
нормальной форме матрицы, можно также воспользоваться следующей формулой:
в жордановой
нормальной форме матрицы, можно также воспользоваться следующей формулой:
![]() .
.
Заметьте, что для определения числа клеток второго
порядка пришлось бы вычислять куб матрицы (пятого порядка!). Используя свойства
жордановой матрицы, мы прекрасно обошлись и без этой громоздкой формулы. Тем
более что в практических задачах, требующих приведения матрицы ![]() к жордановой нормальной форме,
используется и матрица
к жордановой нормальной форме,
используется и матрица ![]() , приводящая
, приводящая ![]() к этой форме. Матрица
к этой форме. Матрица ![]() есть не что иное, как матрица
перехода от исходного базиса к базису из собственных и присоединенных векторов,
поэтому их все равно приходится находить.
есть не что иное, как матрица
перехода от исходного базиса к базису из собственных и присоединенных векторов,
поэтому их все равно приходится находить.
В примерах 2 – 7 требуется найти жорданову нормальную
форму ![]() матрицы
матрицы ![]() и невырожденную матрицу
и невырожденную матрицу ![]() , приводящую
, приводящую ![]() к жордановой нормальной форме.
к жордановой нормальной форме.
Пример 2.
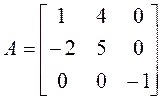 .
.
►Составляем характеристический многочлен и находим его корни:
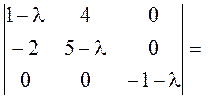
![]() ;
;![]() ,
,
![]() ,
, ![]() .
.
Все корни однократные,
поэтому все клетки будут иметь первый порядок, матрица ![]() имеет
диагональный вид:
имеет
диагональный вид:
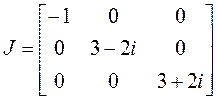 .
.
Находим собственные векторы:
![]()
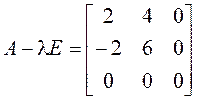 ,
, ![]() ;
;
![]() :
: 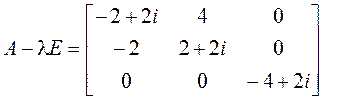 ;
;
![]() ,
, ![]()
(используем алгебраические дополнения к элементам первой строки);
![]() :
: ![]()
(координаты
вектора ![]() – комплексно сопряженные числа
к координатам вектора
– комплексно сопряженные числа
к координатам вектора ![]() , см. пример
§ ). Матрица
, см. пример
§ ). Матрица ![]() , приводящая
, приводящая ![]() к жордановой нормальной форме
– это матрица перехода от исходного базиса к базису из собственных векторов:
к жордановой нормальной форме
– это матрица перехода от исходного базиса к базису из собственных векторов:
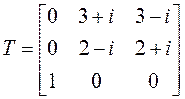 .◄
.◄
Пример 3.
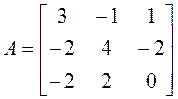 .
.
►1. Составляем характеристический многочлен и находим его корни:
![]()
![]()
![]()
![]()
![]()
![]()
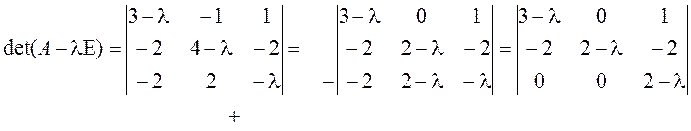 =
=
![]() ;
; ![]() .
.
Один из корней двукратный, ему может соответствовать одна или две клетки. Найдем для этого корня собственные векторы:
![]() :
: 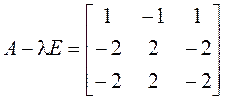 .
(14)
.
(14)
Так
как ![]() , то
, то ![]() , т.е. этому собственному значению
соответствуют два линейно независимых собственных вектора, а значит, жорданова
нормальная форма содержит две клетки с этим собственным значением. Сумма их порядков
равна двум (кратности корня), поэтому они обе имеют первый порядок. Таким
образом,
, т.е. этому собственному значению
соответствуют два линейно независимых собственных вектора, а значит, жорданова
нормальная форма содержит две клетки с этим собственным значением. Сумма их порядков
равна двум (кратности корня), поэтому они обе имеют первый порядок. Таким
образом,
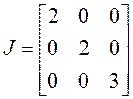 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.