Матрицей перехода от базиса ![]() к базису
к базису ![]() является
следующая:
является
следующая:
а)
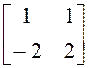 ; б)
; б) 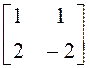 ; в)
; в) 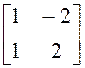 ; г)
; г) 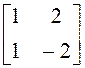 ; д) другой
ответ.
; д) другой
ответ.
ТЕСТ 3 ЛИНЕЙНЫЕ ПРОСТРАНСТВА
ВАРИАНТ 3
Пусть ![]() –
линейное пространство над полем
–
линейное пространство над полем ![]() .
Заданы следующие утверждения: а)
.
Заданы следующие утверждения: а)
![]() ; б)
; б) ![]() ; в)
; в)![]() ; г)
; г) ![]() ; д)
; д)![]() .
.
Из этих утверждений:
1. аксиомами линейного пространства являются:
2. следствиями из аксиом линейного пространства являются:
3. не имеют отношения к линейному пространству:
4. Следующие утверждения верны:
а)
если система ![]() линейно
независима, то равенство
линейно
независима, то равенство ![]() выполняется
в том случае, когда все коэффициенты равны нулю; б) любая линейно зависимая
система содержит линейно зависимую подсистему, не совпадающую с ней самой; в) если
система
выполняется
в том случае, когда все коэффициенты равны нулю; б) любая линейно зависимая
система содержит линейно зависимую подсистему, не совпадающую с ней самой; в) если
система ![]() линейно
независима, то найдутся такие отличные от нуля коэффициенты, что выполняется
равенство
линейно
независима, то найдутся такие отличные от нуля коэффициенты, что выполняется
равенство ![]() ; г) если
какой-либо из элементов системы можно представить в виде линейной комбинации
остальных, то эта система линейно зависима; д) если равенство
; г) если
какой-либо из элементов системы можно представить в виде линейной комбинации
остальных, то эта система линейно зависима; д) если равенство ![]() выполняется при
условии, что все
выполняется при
условии, что все ![]() , то
система
, то
система ![]() линейно независима.
линейно независима.
5.
Из следующих систем векторов
линейно зависимыми являются: а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
6.
В линейном пространстве ![]() задана система
векторов
задана система
векторов ![]() (1). Следующие
утверждения верны: а)
если система (1) линейно независима, то она является базисом; б) если система
(1) линейно независима и
(1). Следующие
утверждения верны: а)
если система (1) линейно независима, то она является базисом; б) если система
(1) линейно независима и ![]() ,
то она является базисом; в) если система (1) является базисом, то любой из
векторов пространства
,
то она является базисом; в) если система (1) является базисом, то любой из
векторов пространства ![]() можно
представить в виде линейной комбинации векторов системы (1); г) если любой из
векторов пространства
можно
представить в виде линейной комбинации векторов системы (1); г) если любой из
векторов пространства ![]() можно
представить в виде линейной комбинации векторов системы (1), то она является
базисом; е).
можно
представить в виде линейной комбинации векторов системы (1), то она является
базисом; е).
7. Следующие утверждения верны: а) в 6-ти мерном линейном пространстве любая система из 7-х векторов линейно независима; б) в 6-ти мерном линейном пространстве любая система из 6-х векторов линейно независима; в) 6-ти мерном линейном пространстве любая система из 6-ти векторов линейно зависима; г) в 6-ти мерном линейном пространстве любая система из 7-ми векторов линейно зависима.
8.
Следующие утверждения верны: а)
подпространство линейного пространства ![]() замкнуто
относительно операций, заданных в
замкнуто
относительно операций, заданных в ![]() ;
б) если
;
б) если ![]() и
и ![]() , то
, то ![]() –
подпространство линейного пространства
–
подпространство линейного пространства ![]() над
над ![]() ; в) если
; в) если ![]() – подпространство
линейного пространства
– подпространство
линейного пространства ![]() над
над ![]() , то
, то ![]() ..
..
9. Если ранг матрицы, составленной из координатных столбцов векторов, равен их количеству, то эти векторы: а) линейно зависимы; б) линейно независимы; в) такого не может быть.
10. Матрицей перехода от базиса ![]() к базису
к базису ![]() является
следующая:
является
следующая:
а) 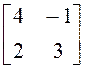 ;
б)
;
б) 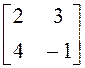 ; в)
; в) 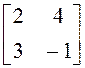 ; г)
; г) 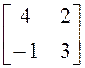 ; д) другой
ответ.
; д) другой
ответ.
ТЕСТ 3 ЛИНЕЙНЫЕ ПРОСТРАНСТВА
ВАРИАНТ 4
Пусть ![]() –
линейное пространство над полем
–
линейное пространство над полем ![]() .
Заданы следующие утверждения: а)
.
Заданы следующие утверждения: а)
![]() ; б)
; б) ![]() ; в)
; в)![]() ; г)
; г) ![]() ; д)
; д) ![]() ; е)
; е)![]() .
.
Из этих утверждений:
1. аксиомами линейного пространства являются:
2. следствиями из аксиом линейного пространства являются:
3. не имеют отношения к линейному пространству:
4. Следующие утверждения верны:
а)
любая подсистема линейно независимой системы линейно независима; б) любая
линейно зависимая система содержит ![]() ;
в) если любой из элементов системы можно представить в виде линейной комбинации
остальных, то эта система линейно зависима; г) система, содержащая линейно
независимую подсистему, линейно независима; д) если система
;
в) если любой из элементов системы можно представить в виде линейной комбинации
остальных, то эта система линейно зависима; г) система, содержащая линейно
независимую подсистему, линейно независима; д) если система ![]() линейно
независима, то равенство
линейно
независима, то равенство ![]() выполняется
только в том случае, когда все коэффициенты равны нулю.
выполняется
только в том случае, когда все коэффициенты равны нулю.
5.
Из следующих систем функций
линейно зависимыми являются: а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
6.
В линейном пространстве ![]() задана система
векторов
задана система
векторов ![]() (1). Следующие
утверждения верны: а)
если система (1) линейно независима и
(1). Следующие
утверждения верны: а)
если система (1) линейно независима и ![]() , то она является
базисом; б) если система (1) является базисом, то она линейно независима; в) если
, то она является
базисом; б) если система (1) является базисом, то она линейно независима; в) если
![]() , то система (1)
является базисом; г) если система (1) является базисом, то
, то система (1)
является базисом; г) если система (1) является базисом, то ![]() .
.
7. Следующие утверждения верны: а) в 7-ми мерном линейном пространстве любая система из 6-ти векторов линейно зависима; б) в 7-ми мерном линейном пространстве существует линейно независимая система из 6-ти векторов; в) в 7-ми мерном линейном пространстве существует линейно независимая система из 7-ми векторов.
8.
Следующие утверждения верны: а)
непустое подмножество линейного пространства ![]() , замкнутое
относительно операций, заданных в
, замкнутое
относительно операций, заданных в ![]() ,
является его подпространством; б) любое подпространство линейного пространства
является линейной оболочкой некоторой системы векторов; в) линейная оболочка
произвольной системы векторов линейного пространства является его
подпространством.
,
является его подпространством; б) любое подпространство линейного пространства
является линейной оболочкой некоторой системы векторов; в) линейная оболочка
произвольной системы векторов линейного пространства является его
подпространством.
9. . Если ранг матрицы, составленной из координатных столбцов векторов, больше их количества, то эти векторы: а) линейно зависимы; б) линейно независимы; в) такого не может быть.
10. Матрицей перехода от базиса ![]() к базису
к базису ![]() : является
следующая:
: является
следующая:
а)
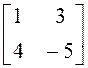 ; б)
; б) 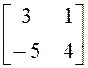 ; в)
; в) 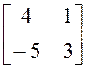 ; г)
; г) 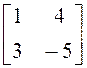 ; д) другой
ответ.
; д) другой
ответ.
ТЕСТ 3 ЛИНЕЙНЫЕ ПРОСТРАНСТВА
ВАРИАНТ 5
Пусть ![]() –
линейное пространство над полем
–
линейное пространство над полем ![]() .
Заданы следующие утверждения: а)
.
Заданы следующие утверждения: а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д)![]() ; е)
; е) ![]() .
.
Из этих утверждений:
1. аксиомами линейного пространства являются:
2. следствиями из аксиом линейного пространства являются:
3. не имеют отношения к линейному пространству:
4. Следующие утверждения верны:
а)
любая подсистема линейно независимой системы линейно независима; б) если
система линейно зависима, то какой-либо из ее элементов можно представить в
виде линейной комбинации остальных; в) если система содержит ![]() , то она линейно
зависима; г) если равенство
, то она линейно
зависима; г) если равенство ![]() выполняется
при условии, что все
выполняется
при условии, что все ![]() , то
система
, то
система ![]() линейно
зависима; д) если система
линейно
зависима; д) если система ![]() линейно
независима, то найдутся такие отличные от нуля коэффициенты, что выполняется равенство
линейно
независима, то найдутся такие отличные от нуля коэффициенты, что выполняется равенство
![]() .
.
5.
Из следующих систем векторов
линейно зависимыми являются: а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д)![]() .
.
6.
В линейном пространстве ![]() задана система
векторов
задана система
векторов ![]() (1). Следующие
утверждения верны: а)
если система (1) линейно независима и
(1). Следующие
утверждения верны: а)
если система (1) линейно независима и ![]() , то она
является базисом; б) если любой из векторов пространства
, то она
является базисом; б) если любой из векторов пространства ![]() можно представить
в виде линейной комбинации векторов системы (1), то она является базисом; в) если
система (1) является базисом, то она линейно независима; г) если система (1)
линейно независима, то она является базисом.
можно представить
в виде линейной комбинации векторов системы (1), то она является базисом; в) если
система (1) является базисом, то она линейно независима; г) если система (1)
линейно независима, то она является базисом.
7. Следующие утверждения верны: а) в 5-ти мерном линейном пространстве любая система из 6-х векторов линейно зависима; б) в 5-ти мерном линейном пространстве любая система из 4-х векторов линейно независима; в) в 5-ти мерном линейном пространстве существует линейно независимая система из 4-х векторов.
8.
Следующие утверждения верны: а)
если ![]() и
и ![]() , то
, то ![]() –
подпространство линейного пространства
–
подпространство линейного пространства ![]() над
над ![]() ; б) если
; б) если ![]() , то
, то ![]() – подпространство
линейного пространства
– подпространство
линейного пространства ![]() ; в) если
; в) если
![]() –
подпространство линейного пространства
–
подпространство линейного пространства ![]() над
над ![]() , то
, то ![]() .
.
9. Если ранг матрицы, составленной из координатных столбцов векторов, меньше их количества, то эти векторы: а) линейно зависимы; б) линейно независимы; в) такого не может быть.
10. Матрицей перехода от базиса ![]() к базису
к базису ![]() : является
следующая:
: является
следующая:
а)
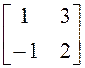 ; б)
; б) 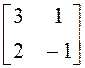 ; в)
; в) 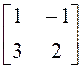 ; г)
; г) 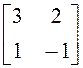 ; д) другой
ответ.
; д) другой
ответ.
ТЕСТ 3 ЛИНЕЙНЫЕ ПРОСТРАНСТВА
ВАРИАНТ 6
Пусть ![]() –
линейное пространство над полем
–
линейное пространство над полем ![]() .
Заданы следующие утверждения: а)
.
Заданы следующие утверждения: а)
![]() ; б)
; б) ![]() ; в)
; в)![]() ; г)
; г) ![]() ; д)
; д) ![]() ; е)
; е) ![]() .
.
Из этих утверждений:
1. аксиомами линейного пространства являются:
2. следствиями из аксиом линейного пространства являются:
3. не имеют отношения к линейному пространству:
4. Следующие утверждения верны:
а)
система, содержащая линейно независимую подсистему, линейно независима; б) если
любой из элементов системы можно представить в виде линейной комбинации
остальных, то эта система линейно зависима; в) любая линейно зависимая система
содержит линейно зависимую подсистему, не совпадающую с ней самой; г) если
система линейно зависима, то любой из ее элементов можно представить в виде
линейной комбинации остальных; д) если равенство ![]() выполняется при
условии, что все
выполняется при
условии, что все ![]() , то
система
, то
система ![]() линейно
независима; е) если система
линейно
независима; е) если система ![]() линейно
независима, то найдутся такие отличные от нуля коэффициенты, что выполняется равенство
линейно
независима, то найдутся такие отличные от нуля коэффициенты, что выполняется равенство
![]() .
.
5.
Из следующих систем функций
линейно зависимыми являются: а)
![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() .
.
6.
В линейном пространстве ![]() задана система
векторов
задана система
векторов ![]() (1). Следующие
утверждения верны: а)
если система (1) является базисом, то
(1). Следующие
утверждения верны: а)
если система (1) является базисом, то ![]() ; б) если
система (1) является базисом, то она линейно независима; в) если система (1)
является базисом, то любой из векторов пространства
; б) если
система (1) является базисом, то она линейно независима; в) если система (1)
является базисом, то любой из векторов пространства ![]() можно представить
в виде линейной комбинации векторов системы (1); г) если
можно представить
в виде линейной комбинации векторов системы (1); г) если ![]() , то система (1)
является базисом; д) если любой из векторов пространства
, то система (1)
является базисом; д) если любой из векторов пространства ![]() можно представить
в виде линейной комбинации векторов системы (1), то она является базисом; е)
если система (1) линейно независима, то она является базисом; ж) если система
(1) линейно независима и
можно представить
в виде линейной комбинации векторов системы (1), то она является базисом; е)
если система (1) линейно независима, то она является базисом; ж) если система
(1) линейно независима и ![]() ,
то она является базисом.
,
то она является базисом.
7. Следующие утверждения верны: а) в 6-ти мерном линейном пространстве любая система из 6-ти векторов линейно зависима; б) в 6-ти мерном линейном пространстве существует линейно независимая система из 5-ти векторов; в) в 6-ти мерном линейном пространстве любая система из 7-ми векторов линейно независима.
8.
Следующие утверждения верны: а)
если ![]() , то
, то ![]() –
подпространство линейного пространства
–
подпространство линейного пространства ![]() над
над ![]() ; б) если
; б) если
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.