41.
1. Линейный оператор ![]() в
некотором базисе пространства
в
некотором базисе пространства ![]() имеет
матрицу А. Найдите собственные векторы этого оператора, если А =
имеет
матрицу А. Найдите собственные векторы этого оператора, если А = 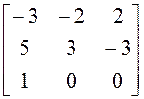 .
.
2. Найдите ![]() и
и ![]() , если
, если ![]() ,
, ![]() ,
, 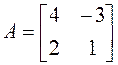 .
.
3. Пользуясь
правилом Крамера, решите систему уравнений 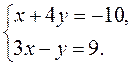 .
.
4. При помощи
матричного критерия исследуйте на линейную зависимость систему векторов 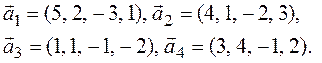 .
.
5. Исследуйте на
знакоопределенность квадратичную форму: ![]()
42.
1.Линейный оператор ![]() в
некотором базисе пространства
в
некотором базисе пространства ![]() имеет
матрицу А. Найдите собственные векторы этого оператора, если А =
имеет
матрицу А. Найдите собственные векторы этого оператора, если А = 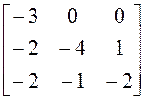 .
.
2. Найдите ![]() ,
если
,
если ![]() ,
, 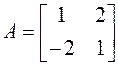 .
.
3. Пользуясь
правилом Крамера, решите систему уравнений 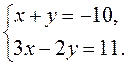 .
.
4. При помощи
матричного критерия исследуйте на линейную зависимость систему векторов 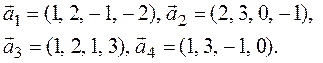 .
.
5. Исследуйте на
знакоопределенность квадратичную форму: ![]()
43.
1. Линейный оператор ![]() в
некотором базисе пространства
в
некотором базисе пространства ![]() имеет
матрицу А. Найдите собственные векторы этого оператора, если А =
имеет
матрицу А. Найдите собственные векторы этого оператора, если А = 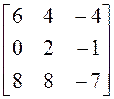 .
.
2. Покажите, что матрица 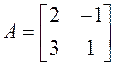 является корнем
многочлена
является корнем
многочлена ![]() .
.
3. Пользуясь правилом
Крамера, решите систему уравнений 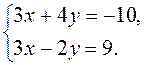 .
.
4. При помощи
матричного критерия исследуйте на линейную зависимость систему векторов 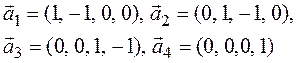 .
.
5. Исследуйте на
знакоопределенность квадратичную форму: ![]()
44.
1.Линейный оператор ![]() в
некотором базисе пространства
в
некотором базисе пространства ![]() имеет
матрицу А. Найдите собственные векторы этого оператора, если А =
имеет
матрицу А. Найдите собственные векторы этого оператора, если А = 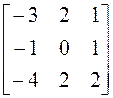 .
.
2. Найдите ранг матрицы 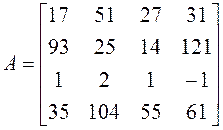 .
.
3. Исследуйте на
совместность систему линейных уравнений. Если она совместна, найдите ее общее и
какое-либо частное решение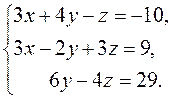
4. При помощи
матричного критерия исследуйте на линейную зависимость систему векторов 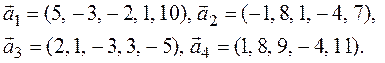 .
.
5. Исследуйте на
знакоопределенность квадратичную форму: ![]()
45. Линейный оператор ![]() в
некотором базисе пространства
в
некотором базисе пространства ![]() имеет
матрицу А. Найдите собственные векторы этого оператора, если А =
имеет
матрицу А. Найдите собственные векторы этого оператора, если А = 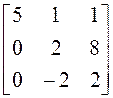 .
.
2. Пользуясь правилом
Крамера, решите систему уравнений 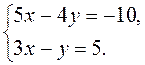 .
.
3. Методом
элементарных преобразований вычислите определитель 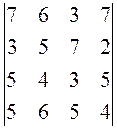 .
.
4. Запишите матрицу
перехода от базиса ![]() к базису
к базису ![]() .
.
5. Исследуйте на
знакоопределенность квадратичную форму: ![]()
46.
1. Линейный оператор ![]() в
некотором базисе пространства
в
некотором базисе пространства ![]() имеет
матрицу А. Найдите собственные векторы этого оператора, если А =
имеет
матрицу А. Найдите собственные векторы этого оператора, если А = 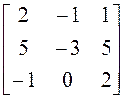 .
.
2.
Используя алгебраические
дополнения, найдите обратную матрицу для матрицы 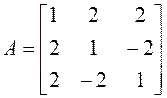 .
.
3.
Исследуйте на совместность систему
линейных уравнений. Если она совместна, найдите ее общее и какое-либо частное
решение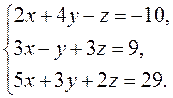
4.
Запишите матрицу перехода от
базиса ![]() к базису
к базису ![]() .
.
5.
Исследуйте на знакоопределенность
квадратичную форму: ![]()
47.
1. Линейный оператор в некотором базисе пространства ![]() имеет матрицу А.
Найдите собственные векторы этого оператора, если А =
имеет матрицу А.
Найдите собственные векторы этого оператора, если А = 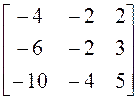 .
.
2.
Используя алгебраические
дополнения, найдите обратную матрицу для матрицы 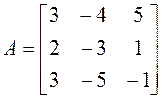
3.
Исследуйте на совместность систему
линейных уравнений. Если она совместна, найдите ее общее и какое-либо частное
решение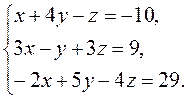
4.
Запишите матрицу перехода от
базиса ![]() к базису
к базису ![]() .
.
5.
Исследуйте на знакоопределенность
квадратичную форму: ![]()
48.
1. Линейный оператор ![]() в
некотором базисе пространства
в
некотором базисе пространства ![]() имеет
матрицу А. Найдите собственные векторы этого оператора, если А =
имеет
матрицу А. Найдите собственные векторы этого оператора, если А = 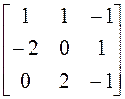 .
.
2. Используя алгебраические дополнения, найдите обратную
матрицу для матрицы 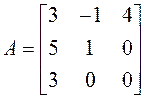 .
.
3.
Исследуйте на совместность систему линейных уравнений. Если она совместна, найдите
ее общее и какое-либо частное решение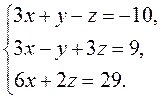
4.
Запишите матрицу перехода от базиса ![]() к
базису
к
базису ![]() .
.
5. Исследуйте на
знакоопределенность квадратичную форму: ![]()
501.
Линейный оператор ![]() в
некотором базисе пространства
в
некотором базисе пространства ![]() имеет
матрицу А. Найдите собственные векторы этого оператора, если
имеет
матрицу А. Найдите собственные векторы этого оператора, если
А =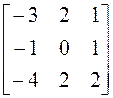 .
.
502.
Линейный оператор ![]() в
некотором базисе пространства
в
некотором базисе пространства ![]() имеет
матрицу А. Найдите собственные векторы этого оператора, если
имеет
матрицу А. Найдите собственные векторы этого оператора, если
А =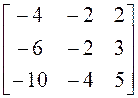 .
.
503.
Линейный оператор ![]() в
некотором базисе пространства
в
некотором базисе пространства ![]() имеет
матрицу А. Найдите собственные векторы этого оператора, если
имеет
матрицу А. Найдите собственные векторы этого оператора, если
А =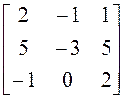 .
.
504.
Линейный оператор ![]() в
некотором базисе пространства
в
некотором базисе пространства ![]() имеет
матрицу А. Найдите собственные векторы этого оператора, если
имеет
матрицу А. Найдите собственные векторы этого оператора, если
А =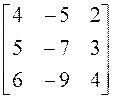 .
.
505.
Проверьте, приводится ли заданная
матрица к диагональному виду над полем действительных чисел. Если приводится,
найдите этот диагональный вид ( матрицу ![]() ) и невырожденную
матрицу Т, приводящую нему, если
) и невырожденную
матрицу Т, приводящую нему, если
А = 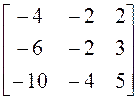 .
.
506.
Проверьте, приводится ли заданная
матрица к диагональному виду над полем действительных чисел. Если приводится,
найдите этот диагональный вид ( матрицу ![]() ) и невырожденную
матрицу Т, приводящую нему, если
) и невырожденную
матрицу Т, приводящую нему, если
А = 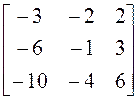 .
.
507.
Проверьте, приводится ли заданная
матрица к диагональному виду над полем действительных чисел. Если приводится,
найдите этот диагональный вид ( матрицу ![]() ) и невырожденную
матрицу Т, приводящую нему, если
) и невырожденную
матрицу Т, приводящую нему, если
А = 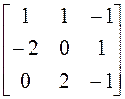 .
.
508. Проверьте, приводится ли заданная матрица к диагональному виду
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.