МАТРИЦЫ ВАРИАНТ 1
1. Даны матрицы 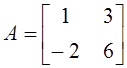 и
и 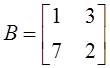 . Матрица
. Матрица ![]() равна:
равна:
а) 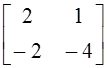 ; б)
; б) 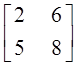 ; в)
; в) 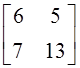 ; г) другой
ответ.
; г) другой
ответ.
2. Для матрицы 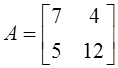 транспонированной
матрицей является:
транспонированной
матрицей является:
а) 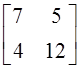 ; б)
; б) 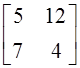 ; в)
; в) 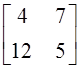 ; г) другой
ответ.
; г) другой
ответ.
3. Даны матрицы 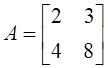 и
и 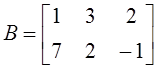 . Определены
следующие произведения: а)
. Определены
следующие произведения: а) ![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]() , д)
, д) ![]() , е)
, е) ![]() , ж)
, ж) ![]() , з)
, з) ![]() .
.
4. Известно, что 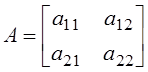 . Матрица
. Матрица ![]() равна: а)
равна: а) 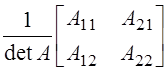 ; б)
; б)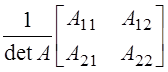 ; в)
; в) 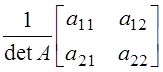 ; г) другой
ответ.
; г) другой
ответ.
5. Для всех
матриц, для которых выполнимы приведенные операции, следующие утверждения верны
(![]() - некоторое
число, отличное от нуля):
- некоторое
число, отличное от нуля):
а)![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]() .
.
6. Задана матрица
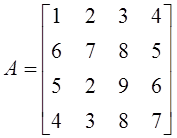 .
. ![]() равен: а)
равен: а)![]() ; б)
; б) ![]() ; в)
; в)![]() ; г) другой
ответ.
; г) другой
ответ.
7. Если в определителе первую строку умножить на 10, а второй столбец разделить на 2, то этот определитель: а) умножится на 10; б) разделится на 2; в) умножится на 5, г) другой ответ.
8. Если в определителе поменять местами два первых столбца, то этот определитель: а) умножится на 2; б) не изменится; в) поменяет знак; г) другой ответ.
9. Следующие
утверждения верны: а) если
определитель содержит строку, полностью состоящую из нулей, то он равен нулю;
б) если ![]() , то
, то ![]() ; в) ?если определитель
равен нулю, то он содержит пропорциональные строки.
; в) ?если определитель
равен нулю, то он содержит пропорциональные строки.
10. Если в определителе к пятому столбцу прибавить третий, умноженный на 12, то определитель при этом: а) умножится на 12; б) разделится на 12; в) не изменится; г) другой ответ.
МАТРИЦЫ ВАРИАНТ 2
1. Даны матрицы 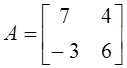 и
и 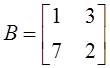 . Матрица
. Матрица ![]() равна:
равна:
а) 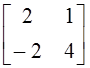 ; б)
; б) 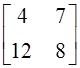 ; в)
; в) 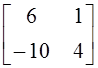 ; г) другой
ответ.
; г) другой
ответ.
2. Матрица ![]() определена
для следующих матриц: а)
определена
для следующих матриц: а) 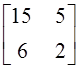 ; б)
; б)  ; в)
; в) 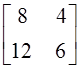 ; г) таких
нет.
; г) таких
нет.
3. Даны матрицы 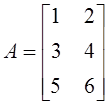 и
и 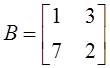 . Определены
следующие произведения: а)
. Определены
следующие произведения: а) ![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]() , д)
, д) ![]() , е)
, е) ![]() , ж)
, ж) ![]() , з)
, з) ![]() .
.
4. Для всех
матриц, для которых выполнимы приведенные операции, следующие утверждения верны
(![]() - некоторое
число, отличное от нуля):
- некоторое
число, отличное от нуля):
а) ![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]() .
.
5. Задана матрица
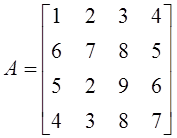 .
. ![]() равен: а)
равен: а)![]() ; б)
; б) ![]() ; в)
; в)![]() ; г)другой
ответ.
; г)другой
ответ.
6. При транспонировании матрицы ее определитель: а) умножится на 2; б) не изменится в) поменяет знак; г) другой ответ
7. Следующие
утверждения верны: а) если определитель равен
нулю, то он содержит строку, полностью состоящую из нулей; б) если ![]() , то
, то ![]() ; в) если определитель содержит пропорциональные строки,
то он равен нулю.
; в) если определитель содержит пропорциональные строки,
то он равен нулю.
8. Если в определителе к первой строке прибавить седьмую, умноженную на 3, то определитель при этом: а) не изменится; б) поменяет знак; в) умножится на 3; г) разделится на 3; д) другой ответ.
9. Известно, что
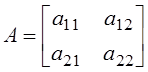 . Матрица
. Матрица ![]() равна: а)
равна: а) 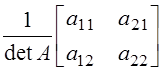 ; б)
; б)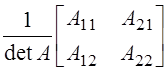 ; в)
; в) 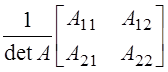 ; г) другой
ответ.
; г) другой
ответ.
10. Матрица определена для следующих матриц:
а) 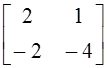 ; б) ; в)
; б) ; в) 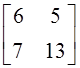 ; г) таких
нет.
; г) таких
нет.
МАТРИЦЫ ВАРИАНТ 5
1. Даны матрицы 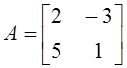 и
и 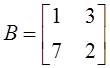 . Матрица
. Матрица ![]() равна:
равна:
а) 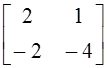 ; б)
; б) 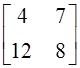 ; в)
; в) 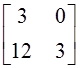 ; г) другой
ответ.
; г) другой
ответ.
2. Для матрицы 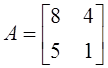 транспонированной
матрицей является: а)
транспонированной
матрицей является: а) 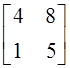 ; б)
; б) 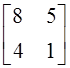 ; в)
; в) 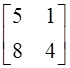 ; г) другой
ответ.
; г) другой
ответ.
3. Даны матрицы 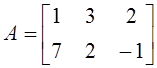 и
и 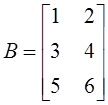 . Определены
следующие произведения: а)
. Определены
следующие произведения: а) ![]() ,б)
,б) ![]() , в)
, в) ![]() , г)
, г) ![]() , д)
, д) ![]() , е)
, е) ![]() , ж)
, ж) ![]() , з)
, з) ![]() .
.
4. Известно, что 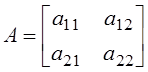 . Матрица
. Матрица ![]() равна: а)
равна: а) 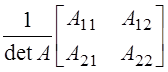 ; б)
; б) 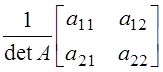 ; в)
; в) 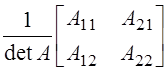 ; г) другой
ответ.
; г) другой
ответ.
5. Для всех
матриц, для которых выполнимы приведенные операции, следующие утверждения верны
(![]() - некоторое
число, отличное от нуля):
- некоторое
число, отличное от нуля):
а) ![]() , б)
, б) ![]() , в)
, в) ![]() , г)
, г) ![]() .
.
6. Задана матрица
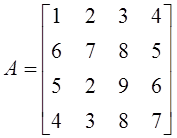 .
. ![]() равно: а)
равно: а)![]() ; б)
; б)![]() ; в)
; в) 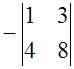 .
.
7. Если в определителе поменять местами третий и четвертый столбцы, то этот определитель: а) умножится на 2; б) не изменится; в) поменяет знак; г) другой ответ.
8. Следующие утверждения верны: а) если определитель равен нулю, то он содержит нулевую строку; б) определитель суммы матриц равен сумме их определителей; в) если определитель содержит пропорциональные строки, то он равен нулю.
9. Матрица ![]() определена
для следующих матриц: а)
определена
для следующих матриц: а) 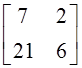 ; б)
; б) 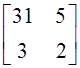 ; в)
; в) 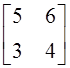 ; г) таких
нет.
; г) таких
нет.
10. Если в определителе к первому столбцу прибавить пятый, умноженный на 7, то определитель при этом: а) умножится на 7; б) разделится на 7; в) не изменится; г) поменяет знак; д) другой ответ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.