ТЕСТ № 3 Прямая и плоскость (7-е занятие)
Тренировочный вариант
Заданы уравнения:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() , г)
, г)![]() ; д)
; д) ![]() ; е)
; е) ![]() ; ж)
; ж)![]() ; з)
; з)![]() ; и)
; и) ![]() ; к)
; к)![]() ; л)
; л) ![]() ; м)
; м)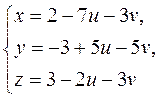 ; н)
; н) 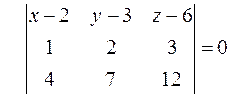 ; о)
; о) 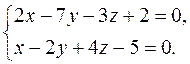
1. Из перечисленных уравнений прямую в пространстве задают следующие:
2. Из перечисленных уравнений плоскость задают следующие:
3. Если для плоскости заданы два вектора, параллельных ей, но между собой неколлинеарных, и точка, то по этим данным составляются следующие уравнения этой плоскости: а) векторное параметрическое; б) параметрические; в) общее; г) в виде определителя; д) другой ответ.
4. Если для плоскости заданы нормальный вектор и точка, то по этим данным составляются следующие уравнения этой плоскости: а) векторное параметрическое; б) параметрические; в) общее; г) другой ответ.
5.
Направляющим вектором прямой ![]() является вектор а)
является вектор а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() , г)
, г) ![]() ; д) другой ответ.
; д) другой ответ.
6.
Направляющим вектором прямой ![]() является вектор:
является вектор:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() , г)
, г) ![]() ; д) другой ответ.
; д) другой ответ.
7.
Нормальным вектором плоскости ![]() является вектор:
является вектор:
![]() ;
б)
;
б) ![]() ; в)
; в) ![]() , г)
, г) ![]() ; д) другой ответ.
; д) другой ответ.
8.
Направляющим вектором прямой ![]() является вектор:
является вектор:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() , г)
, г) ![]() ; д) другой ответ.
; д) другой ответ.
9.
Нормальным вектором плоскости ![]() является вектор: а)
является вектор: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() , г) другой ответ.
, г) другой ответ.
10. Чтобы составить общее уравнение плоскости, для нее следует знать: а) нормальный вектор и точку; б) два неколлинеарных вектора, параллельных этой плоскости, и точку; в) другой ответ.
11. Чтобы составить параметрические уравнения плоскости, для нее следует знать: а) нормальный вектор и точку; б) два неколлинеарных вектора, параллельных этой плоскости, и точку; в) другой ответ.
12. Одна из точек прямой ![]() имеет
следующие координаты: а)
имеет
следующие координаты: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() , г)
, г) ![]() ; д) другой ответ.
; д) другой ответ.
13. Одна из точек прямой ![]() имеет
следующие координаты:
имеет
следующие координаты:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() , г)
, г) ![]() ; д) другой ответ.
; д) другой ответ.
14. Одна из точек прямой ![]() имеет
следующий радиус-вектор: а)
имеет
следующий радиус-вектор: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() , г)
, г) ![]() ; д) другой ответ.
; д) другой ответ.
15. Для прямой ![]() набор
(7;9;7) задаёт: а) направляющий вектор; б)
нормальный вектор; в) точку, принадлежащую прямой.
набор
(7;9;7) задаёт: а) направляющий вектор; б)
нормальный вектор; в) точку, принадлежащую прямой.
16. Для прямой ![]() набор
(-5;3;3) задаёт:
набор
(-5;3;3) задаёт:
а) направляющий вектор; б) нормальный вектор; в) точку, принадлежащую прямой.
17. Для плоскости ![]() набор
(7;9;7) задаёт: а) вектор, параллельный
плоскости; б) нормальный вектор; в) точку, принадлежащую плоскости.
набор
(7;9;7) задаёт: а) вектор, параллельный
плоскости; б) нормальный вектор; в) точку, принадлежащую плоскости.
18. Для прямой ![]() набор
(-5;3;3) задаёт:
набор
(-5;3;3) задаёт:
а) направляющий вектор; б) нормальный вектор; в) точку, принадлежащую прямой.
19. Для прямой ![]() набор
(7;9;7) задаёт: а) направляющий вектор; б)
нормальный вектор; в) точку, принадлежащую прямой.
набор
(7;9;7) задаёт: а) направляющий вектор; б)
нормальный вектор; в) точку, принадлежащую прямой.
20. Для прямой ![]() вектор
вектор ![]() является: а) направляющим; б) нормальным;
в) радиус-вектором некоторой точки этой прямой, г) другой ответ.
является: а) направляющим; б) нормальным;
в) радиус-вектором некоторой точки этой прямой, г) другой ответ.
21. Для прямой ![]() вектор
вектор ![]() является:
является:
а) направляющим; б) нормальным; в) радиус-вектором некоторой точки этой прямой, г) другой ответ
22. Для плоскости ![]() набор
(2;-3;3) задаёт: а) вектор, параллельный
плоскости; б) нормальный вектор; в) точку, принадлежащую плоскости; г) другой
ответ.
набор
(2;-3;3) задаёт: а) вектор, параллельный
плоскости; б) нормальный вектор; в) точку, принадлежащую плоскости; г) другой
ответ.
23. Для плоскости ![]() набор
(-7;5;-2) задаёт: а) вектор, параллельный
плоскости; б) нормальный вектор; в) точку, принадлежащую плоскости; г) другой
ответ.
набор
(-7;5;-2) задаёт: а) вектор, параллельный
плоскости; б) нормальный вектор; в) точку, принадлежащую плоскости; г) другой
ответ.
24. Для плоскости ![]() вектор
вектор![]() является: а) вектором, параллельным
плоскости; б) нормальным вектором; в) радиус-вектором некоторой точки; г)
другой ответ.
является: а) вектором, параллельным
плоскости; б) нормальным вектором; в) радиус-вектором некоторой точки; г)
другой ответ.
25. Для плоскости ![]() вектор
вектор![]() является: а) вектором, параллельным
плоскости; б) нормальным вектором; в) радиус-вектором некоторой точки; г)
другой ответ.
является: а) вектором, параллельным
плоскости; б) нормальным вектором; в) радиус-вектором некоторой точки; г)
другой ответ.
Заданы следующие пары
плоскостей: а) ![]() и
и ![]() ;
;
б) ![]() и
и ![]() ;
;
в) ![]() и
и ![]() ;
;
г) ![]() и
и ![]() .
.
26. Из этих пар пересекающимися являются:
27. Из этих пар параллельными являются:
28. Из этих пар совпадающими являются:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.