Приведение уравнений линий и поверхностей второго порядка к каноническому виду

§. 5. Приведение уравнений линий и поверхностей

второго порядка к каноническому виду

Известно, что для любой квадратичной формы на конечном действительном евклидовом пространстве в этом пространстве существует ортонормированный базис, в котором рассматриваемая квадратичная форма имеет канонический вид. Используя этот факт, любую линию или поверхность второго порядка можно привести к каноническому виду по следующему плану.

1.  Для квадратичной части уравнения (т. е. квадратичной формы) находим канонический вид и ортогональное преобразование переменных, приводящее квадратичную форму к этому каноническому виду.

2.  Подставляем выражение старых переменных через новые в исходное уравнение. При этом квадратичная часть переходит в известный нам канонический вид, в котором коэффициенты при квадратах совпадают с собственными значениями ее матрицы, свободный член не меняется, линейная часть преобразуется непосредственно.

3.  Получили уравнение, не содержащее произведений переменных. С помощью преобразования параллельного переноса избавляемся от лишних слагаемых первых степеней и тем самым окончательно приводим уравнение к каноническому виду.

Если линия или поверхность второго порядка имеет центр симметрии, то решение задачи можно существенно упростить, поменяв местами 1-й и третий пункты, а второй тогда совсем исчезает.

Для того чтобы точка  была центром симметрии поверхности второго порядка , необходимо и достаточно, чтобы координаты этой точки удовлетворяли системе линейных уравнений

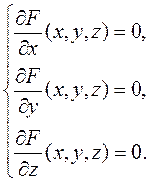                                          (5. 3)

Если с помощью параллельного переноса поместить начало координат в центр симметрии поверхности второго порядка, то при этом: квадратичная часть ее уравнения не изменится; слагаемые первой степени пропадут; свободный член нового уравнения можно найти по формуле

.                                      (5.4)

Аналогичные утверждения справедливы и для линий второго порядка (подробно обоснование см., например, в []).

Пример 1. Определить вид линии второго порядка, приведя ее уравнение к каноническому виду, и нарисовать эту линию, если ее уравнение имеет вид

.                              (5.5)

►В первую очередь проверим, имеет ли эта линия центр симметрии. Составляем систему линейных уравнений (5.3)

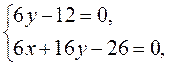
из которой находим: . Поместим с помощью параллельного переноса начало координат в точку  (если в задаче используются несколько систем координат, то обязательно надо указывать, в какой именно из них вы даете координаты точки). По формуле (5.4) (подставляем координаты  в левую часть (5.5)) находим . После преобразования параллельного переноса уравнение линии примет вид .

Теперь приведем к каноническому виду квадратичную часть уравнения  (т. е. квадратичную форму) с помощью ортогонального преобразования переменных. Для этого записываем матрицу этой квадратичной формы и находим ее собственные значения:

,   ,   .

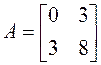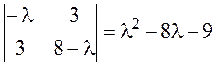Для нахождения первого собственного вектора решаем систему линейных уравнений с матрицей  при : 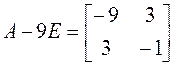, . Чтобы найти второй собственный вектор нет необходимости решать вторую систему. Достаточно вспомнить, что он ортогонален вектору  в силу симметричности матрицы А и что его координаты можно получить, как и в аналитической геометрии, переставив местами координаты вектора  и в одной из них поменяв знак. Итак, . Применим ортогональное преобразование, в результате которого оси новой системы координат будут направлены по собственным векторам. После этого уравнение примет вид (коэффициенты при квадратах совпадают с найденными собственными значениями) , или , которое задает гиперболу с полуосями 1 и 3 и осью  в качестве действительной.

Приступаем к рисованию. На одном рисунке изображаем и старую систему координат, и новую. Намечаем новое начало координат – точку . От этой точки откладываем собственные векторы  и , которые задают направление новых осей. В полученной системе координат рисуем полученную гиперболу (рис.5.1). ◄

Замечания. 1. При таком способе решения нет необходимости выписывать ни преобразование параллельного переноса, ни ортогональное преобразование, т. к. мы и без непосредственной подстановки их в уравнение знаем, как оно преобразуется. Нет необходимости даже собственные векторы нормировать: ортогональное преобразование не нужно, а векторы с целочисленными координатами легче рисовать. Именно поэтому задачу приведения линии второго порядка к каноническому виду в том случае, когда эта линия имеет центр симметрии, сложной не назовешь.