Приведение уравнений линий и поверхностей второго порядка к каноническому виду, страница 2

2. Коэффициенты при квадратах (собственные значения) в каноническом уравнении пишутся в произвольном порядке, а вот собственные векторы в новом базисе имеют соответствующий порядок. При этом новая система координат не обязательно получится правой.

Пример 2. Определить видповерхности второго порядка

, приведя ее уравнение к каноническому виду, и нарисовать эту поверхность.

► Проверяем существование центра симметрии. Для этого вычисляем частные производные и составляем систему вида (5.3):

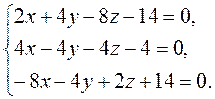
Решаем систему, как обычно: составляем ее расширенную матрицу и преобразуем с помощью элементарных преобразований, применяя их только к строкам. 

.

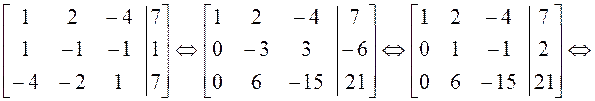
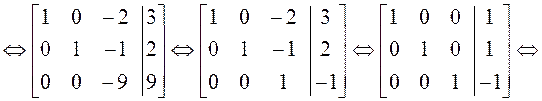Получаем . Считаем .

Приводим к каноническому виду квадратичную часть уравнения  с помощью ортогонального преобразования переменных. Как и в предыдущем примере, записываем матрицу этой квадратичной формы и находим ее собственные значения:

,;   .

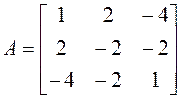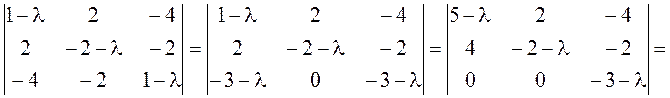
Каноническое уравнение поверхности имеет вид , или , это конус второго порядка, вытянутый вдоль оси .

Ищем собственные векторы:

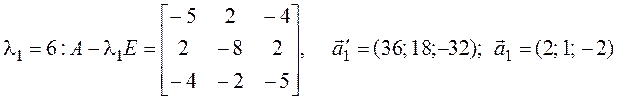
(используем алгебраические дополнения к элементам первой строки).

.

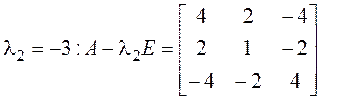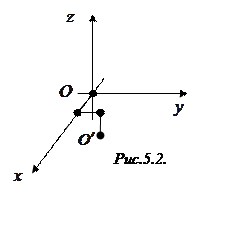Все три уравнения системы пропорциональны, это значит, что существует целая плоскость собственных векторов с собственным значением . Для искомого базиса достаточно взять любые два из них, но взаимно ортогональные. По матрице записываем единственное уравнение системы . Его общим решением является вектор . В качестве вектора  можно взять любое частное решение, например, , а координаты третьего вектора найти из условия , из которого следует, что , т.е. . Полагая , получаем . Можно было и вообще не решать систему для второго собственного значения, а просто устно подобрать два взаимно ортогональных вектора, ортогональных еще и вектору , но это не у всех хорошо получается.

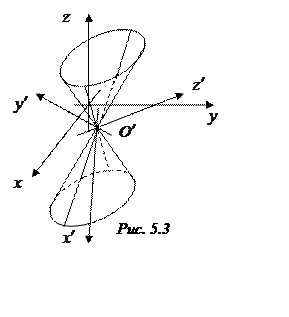
Теперь будем рисовать. Для определения положения точки  из начала координат идем по ломаной, звенья которой параллельны координатным осям. Вначале идем вдоль оси  на одну единицу в положительном направлении, затем от полученной точки передвигаемся на единицу вправо параллельно оси , и, наконец, от последней точки идем на единицу вниз параллельно оси  (рис.5.2). От полученной точки откладываем найденные базисные векторы, которые определяют направления новых осей. В полученной системе координат рисуем конус второго порядка (рис. 5.3).◄

Пример 3. Определить вид поверхности второго порядка, приведя ее уравнение к каноническому виду, и нарисовать эту поверхность, если ее уравнение имеет вид

.

►Опять проверим наличие центра симметрии, для чего составим систему линейных уравнений вида (5.3):

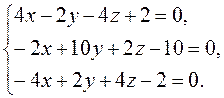
Заметим, что первое и третье уравнения системы пропорциональны, одно из них можно отбросить. Эта система имеет бесчисленное множество решений, значит, поверхность имеет бесчисленное множество центров симметрии. Для решения задачи возьмем любой из них, например,  (то, что это решение системы просто видно невооруженным глазом). Находим .

Приводим к каноническому виду квадратичную часть уравнения  с помощью ортогонального преобразования переменных.

,,   .

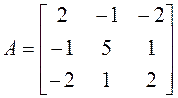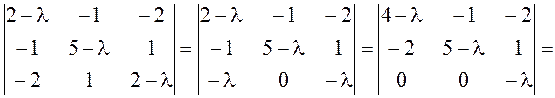
Каноническое уравнение поверхности имеет вид , или , это эллиптический цилиндр.

Ищем собственные векторы:

;

;

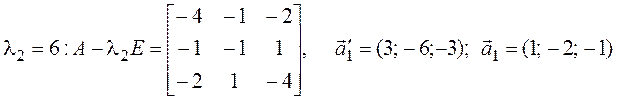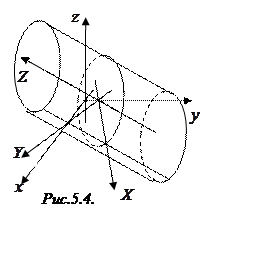
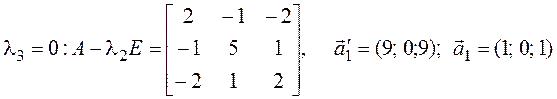
(во всех трех случаях используем алгебраические дополнения к элементам первой строки).

Приступаем к рисованию. В старой системе координат намечаем точку  и от нее откладываем базисные векторы, которые задают направление новых осей. В полученной системе координат рисуем эллиптический цилиндр с образующими, параллельными оси  (рис. 5.4).◄

Пример 4. Определить вид линии второго порядка при помощи приведения уравнение к каноническому виду и нарисовать эту линию, если ее уравнение имеет вид

.

►Попробовав найти центр симметрии, получаем систему

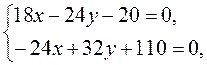
которая оказывается несовместной. Поэтому от слагаемых первой степени избавиться нельзя, начинаем решение задачи с приведения к каноническому виду квадратичной формы. Записываем матрицу этой квадратичной формы и находим ее собственные значения:

,   ,   .

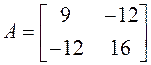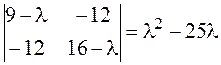Чтобы найти первый собственный вектор, решаем однородную систему линейных уравнений с матрицей  при , т.е., с матрицей , . Второй собственный вектор находим, переставив местами координаты вектора  и в одной из них поменяв знак. Итак, . Длина каждого из векторов равна 5. Нормируем векторы и получаем ортонормированный базис: , . Матрица перехода (она же матрица ортогонального преобразования переменных) имеет вид