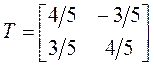Математика \ Аналитическая геометрия и линейная алгебра

Приведение уравнений линий и поверхностей второго порядка к каноническому виду, страница 3

По матрице Tзаписываем ортогональное преобразование переменных:

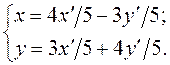(5.6)

Подставляем выражение переменных по формулам (5.6) в исходное уравнение. При этом квадратичная часть переходит в известный нам канонический вид , свободный член не меняется, а чтобы узнать, как изменится линейная часть, подставим формулы (5.6) в уравнение непосредственно, раскроем скобки и приведем подобные.

Замечание. На самом деле коэффициенты линейной части есть линейные комбинации координат векторов и с теми же коэффициентами, что и в исходном уравнении. Например, коэффициент при вычисляется так: , а при – так: .

Таким образом, после преобразования (5.6) приходим к уравнению, или . Полученное уравнение не каноническое, так как наряду с квадратом переменной содержит и ее первую степень. Чтобы избавиться от последней, выделим полный квадрат с переменной , полученное уравнение преобразуем к виду и применим преобразование параллельного переноса . После этого уравнение линии принимает канонический вид , откуда видно, что рассматриваемая линия – парабола, ветви которой направлены в отрицательную сторону оси .

При преобразовании параллельного переноса начало координат переходит в точку , в которой . Значит, . Можно узнать координаты точки и в исходной системе координат. Для этого значения и подставим в формулы (5.6): . Итак, .

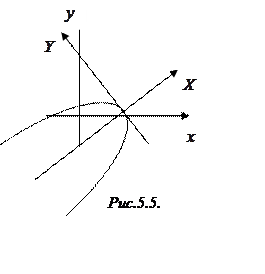
Как обычно, на одном рисунке изображаем и старую систему координат, и новую. Намечаем новое начало координат – точку и от этой точки откладываем собственные векторы и , которые задают направление новых осей. В полученной системе координат рисуем полученную параболу (рис.5.5). ◄

Пример 5. Определить вид поверхности второго порядка при помощи приведения уравнения этой поверхности к каноническому виду и нарисовать эту поверхность, если ее уравнение имеет вид

►Эта поверхность центра симметрии не имеет, в этом вы можете убедиться самостоятельно, поэтому действуем по перу плану.

Приводим к каноническому виду квадратичную часть уравнения с помощью ортогонального преобразования переменных.

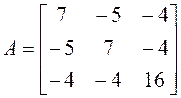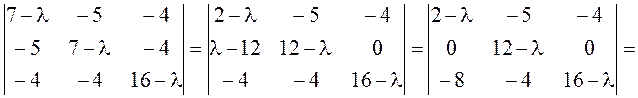
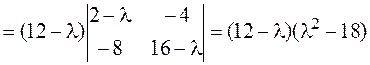
Ищем собственные векторы:

;

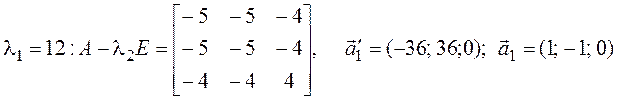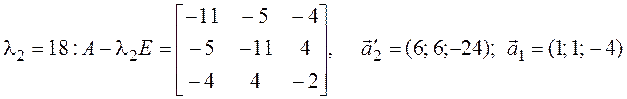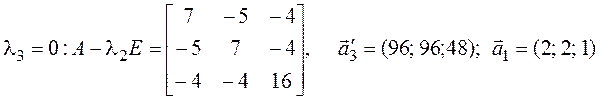
(во всех трех случаях используем алгебраические дополнения к элементам первой строки). Нормируем векторы (каждый делим на его длину) и записываем матрицу перехода к базису из собственных векторов: , , , . Матрица перехода (она же матрица ортогонального преобразования переменных) имеет вид

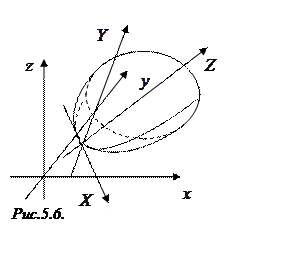
По матрице Tзаписываем ортогональное преобразование переменных:

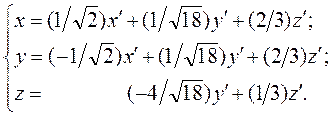
Подставляем выражение переменных в исходное уравнение и получаем , или . После преобразования параллельного переноса уравнение принимает окончательный вид – это эллиптический параболоид. Новое начало координат , или . Поверхность изображена на рис. 5.6.◄

Пример 6. Определить вид поверхности второго порядка при помощи приведения уравнения этой поверхности к каноническому виду и нарисовать эту поверхность, если ее уравнение имеет вид

►Эта поверхность также не имеет центра симметрии. Приводим к каноническому виду квадратичную часть уравнения .

, , .

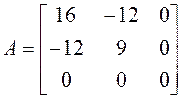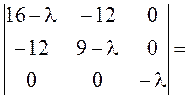
В каноническом виде только один из коэффициентов при квадратах отличен от нуля, поэтому есть опасность, что отличными от нуля останутся два коэффициента при первых степенях. Ищем собственные векторы:

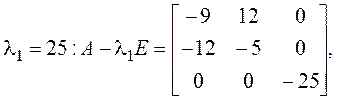
Для собственного значения существует целая плоскость собственных векторов. Все они ортогональны вектору и поэтому имеют координаты при некоторых и . В новом уравнении коэффициенты при и будут равны линейным комбинациям координат векторов и : , . Чтобы получить можно взять, например, . Тогда , . Вектор ортогонален и вектору , и вектору , поэтому и , откуда получаем . Полагая , получаем: , , . 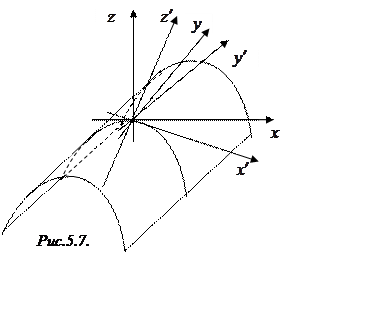Окончательное уравнение имеет вид, или . Это уравнение задает параболический цилиндр (рис.5.7).◄

Задачи

1. Определить вид линии второго порядка и ее расположение относительно системы координат, если в прямоугольной декартовой системе координат эта линия задана уравнением:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

9) ;

10) ;

11) ;

12) ;

13) ;

14) ;

15)

16)

2. Определить вид поверхности второго порядка и ее расположение относительно системы координат, если в прямоугольной декартовой системе координат эта поверхность задана уравнением: