ТЕСТ ПО СОБСТВЕННЫМ ВЕКТОРАМ (10-е занятие)
1.
Линейный оператор ![]() в
базисе
в
базисе ![]() имеет
матрицу
имеет
матрицу 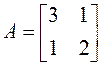 .
Какие из перечисленных векторов будут собственными векторами оператора
.
Какие из перечисленных векторов будут собственными векторами оператора ![]() ?
Какие у них собственные значения? а)
?
Какие у них собственные значения? а)
![]() ;
б)
;
б) ![]() ;
в)
;
в) ![]() ;
г) таких нет.
;
г) таких нет.
2.
Линейный оператор ![]() в
базисе
в
базисе ![]() имеет
матрицу
имеет
матрицу 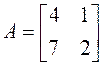 .
Характеристический многочлен этого оператора имеет вид:
.
Характеристический многочлен этого оператора имеет вид:
а) 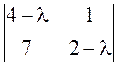 ; б)
; б) 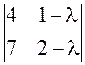 ;
в)
;
в) 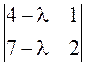 ;
г)
;
г) 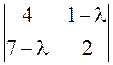 ;
д) другой ответ.
;
д) другой ответ.
3.
Пусть ![]() –
комплексное линейное пространство и пусть линейный оператор
–
комплексное линейное пространство и пусть линейный оператор ![]() имеет
характеристический многочлен
имеет
характеристический многочлен ![]() .
Собственными значениями оператора
.
Собственными значениями оператора ![]() будут
следующие
будут
следующие
Характеристическое
уравнение оператора ![]() выглядит так:
выглядит так:
![]() =0, а характеристическими числами будут корни, Если P= комплексным, то собственное значение только комплексные
корни, какие из них – хз =) : а)
0; б)
=0, а характеристическими числами будут корни, Если P= комплексным, то собственное значение только комплексные
корни, какие из них – хз =) : а)
0; б) ![]() ;
в)
;
в) ![]() ;
г) 2; д) 6; е) другой ответ.
;
г) 2; д) 6; е) другой ответ.
4.
Пусть ![]() –
действительное линейное пространство и пусть линейный оператор
–
действительное линейное пространство и пусть линейный оператор ![]() имеет
характеристический многочлен
имеет
характеристический многочлен ![]() .
Собственными значениями оператора
.
Собственными значениями оператора ![]() будут
следующие ( действительные числа, если правильно помню,
то 2, ноль и корень из -1 не катят): а)
0; б)
будут
следующие ( действительные числа, если правильно помню,
то 2, ноль и корень из -1 не катят): а)
0; б) ![]() ;
в)
;
в) ![]() ;
г) 2; д) 6; е) другой ответ.
;
г) 2; д) 6; е) другой ответ.
5.
Характеристический многочлен
некоторого линейного оператора имеет вид ![]() .
Кратность его собственного значения
.
Кратность его собственного значения ![]() равна
(4 по-моему, так как кратность равна степени скобки,
если я хорошо слушаю лекции и запоминаю их) :
равна
(4 по-моему, так как кратность равна степени скобки,
если я хорошо слушаю лекции и запоминаю их) :
а) 0; б) 1; в) 2; г) 3; д) 4; е) 5; ж) другой ответ.
6.
Пусть кратность собственного значения
![]() линейного
оператора
линейного
оператора ![]() равна
4. Количество линейно независимых собственных векторов с этим собственным
значением может равняться: а)
0; б) 1; в) 2; г) 3; д) 4; е) 5; ж) другой ответ.
равна
4. Количество линейно независимых собственных векторов с этим собственным
значением может равняться: а)
0; б) 1; в) 2; г) 3; д) 4; е) 5; ж) другой ответ.
7.
Теорема 4.15. Пусть ![]() –
линейное пространство над полем Р. Если все
характеристические числа линейного оператора
–
линейное пространство над полем Р. Если все
характеристические числа линейного оператора ![]() принадлежат
полю Р, то в
принадлежат
полю Р, то в ![]() существует
базис, состоящий из собственных и присоединенных векторов оператора f,
причем каждому собственному значению в этом базисе соответствует столько
собственных векторов и присоединенных к ним, какова кратность этого
собственного значения (без доказательства).
существует
базис, состоящий из собственных и присоединенных векторов оператора f,
причем каждому собственному значению в этом базисе соответствует столько
собственных векторов и присоединенных к ним, какова кратность этого
собственного значения (без доказательства).
Пусть
кратность собственного значения ![]() линейного
оператора
линейного
оператора ![]() равна
3 и пусть существует два линейно независимых собственных вектора с этим
собственным значением. Базис линейного пространства
равна
3 и пусть существует два линейно независимых собственных вектора с этим
собственным значением. Базис линейного пространства ![]() ,
состоящий из собственных и присоединенных векторов оператора
,
состоящий из собственных и присоединенных векторов оператора ![]() ,
содержит следующие векторы, соответствующие этому собственному значению:
,
содержит следующие векторы, соответствующие этому собственному значению:
а) три собственных; б) два собственных и один присоединенный; в) один собственный и два присоединенных; г) три присоединенных; д) другой ответ.
8. Правило приведения квадратной матрицы
к диагональному виду над полем Р
СМ пример внизу с.10
1. Составляем характеристический многочлен матрицы А и находим его корни. Если какой-либо из них не принадлежит полю Р, то А к диагональному виду не приводится.
2. Если все характеристические числа принадлежат полю Р,
то для кратных корней проверяем условие ![]() ,
н – размерность матрицы = количеству (кратности) лямд (корней) (для однократных оно выполняется всегда). Если для какого-то
из корней
,
н – размерность матрицы = количеству (кратности) лямд (корней) (для однократных оно выполняется всегда). Если для какого-то
из корней ![]() ,
не выполняется, то А к диагональному виду не
приводится.
,
не выполняется, то А к диагональному виду не
приводится.
3. Если для каждого из собственных значений условие ![]() ,
выполняется, то А к диагональному виду
приводится. Записываем этот диагональный вид – матрицу
,
выполняется, то А к диагональному виду
приводится. Записываем этот диагональный вид – матрицу ![]() ,
располагая на ее главной диагонали собственные значения
,
располагая на ее главной диагонали собственные значения ![]() в
произвольном порядке, причем каждое из значений повторяем столько раз, какова
его кратность.
в
произвольном порядке, причем каждое из значений повторяем столько раз, какова
его кратность.
4. Записываем матрицу Т, приводящую А к диагональному
виду, – матрицу перехода от исходного базиса к базису из собственных векторов,
сохраняя порядок, установленный матрицей ![]() .
.
Линейный
оператор ![]() в
некотором базисе имеет матрицу А. Если этот оператор имеет собственные
значения
в
некотором базисе имеет матрицу А. Если этот оператор имеет собственные
значения ![]() ,
,
![]() ,
,
![]() и
и
![]() ,
то: а) А приводится к диагональному виду( так как корни кратности
1 и для них всегда выполняется условие, но не учитывал, над каким полем) ; б) А не приводится к диагональному
виду; в) для верного ответа не хватает информации.
,
то: а) А приводится к диагональному виду( так как корни кратности
1 и для них всегда выполняется условие, но не учитывал, над каким полем) ; б) А не приводится к диагональному
виду; в) для верного ответа не хватает информации.
9.
Линейный оператор ![]() в
некотором базисе имеет матрицу А. Если этот оператор имеет собственные значения
в
некотором базисе имеет матрицу А. Если этот оператор имеет собственные значения ![]() кратности
3 и
кратности
3 и ![]() ,
причем
,
причем ![]() (дано для 2, так как у корня =2 кратность больше 1, но
не дана размерность матрицы А, а он равен сумме кратностей корней, т е 3+1=4
решаем и получаем), то: а)
А приводится к диагональному виду; б) А неприводится к диагональному виду (4-2 =/= 3) ; в) для верного ответа
не хватает информации.
(дано для 2, так как у корня =2 кратность больше 1, но
не дана размерность матрицы А, а он равен сумме кратностей корней, т е 3+1=4
решаем и получаем), то: а)
А приводится к диагональному виду; б) А неприводится к диагональному виду (4-2 =/= 3) ; в) для верного ответа
не хватает информации.
10. Линейный оператор ![]() в
некотором базисе имеет матрицу А. Если этот оператор имеет собственные
значения
в
некотором базисе имеет матрицу А. Если этот оператор имеет собственные
значения ![]() кратности
3 и
кратности
3 и ![]() ,
причем
,
причем ![]() ,
то (дано для 2, так как у корня =2 кратность больше
1, но не дана размерность матрицы А, а он равен сумме кратностей корней, т е
3+1=4 решаем и получаем)Ж
,
то (дано для 2, так как у корня =2 кратность больше
1, но не дана размерность матрицы А, а он равен сумме кратностей корней, т е
3+1=4 решаем и получаем)Ж
а) А приводится к диагональному виду (4-1 = 3) ; б) А не приводится
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.