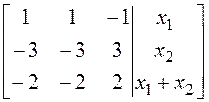 ;
;
Нетрудно
заметить, что эта система имеет решение только в том случае, когда ![]() .
Это значит, только такие собственные векторы имеют присоединенные. Возьмем,
например,
.
Это значит, только такие собственные векторы имеют присоединенные. Возьмем,
например, ![]() , присоединенный к нему найдем,
как решение системы
, присоединенный к нему найдем,
как решение системы
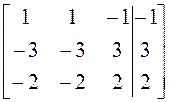 , например,
, например,
![]() , а вектор
, а вектор ![]() Поэтому Собственный вектор
Поэтому Собственный вектор ![]() (частное решение однородной
системы), первый присоединенный (частное решение неоднородной системы с первым
столбцом свободных членов), второй присоединенный
(частное решение однородной
системы), первый присоединенный (частное решение неоднородной системы с первым
столбцом свободных членов), второй присоединенный ![]() –
опять же собственный, неколлинеарный
–
опять же собственный, неколлинеарный ![]() ,
, ![]() . Тогда
. Тогда
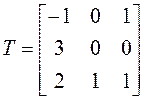 .◄
.◄
Пример 7. Найти жорданову нормальную форму матрицы
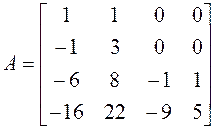 .
.
►1. Составляем характеристический многочлен матрицы А:
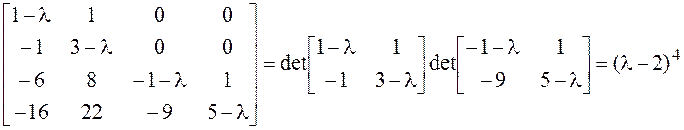 .
.
Таким образом, А имеет единственное собственное
значение ![]() , причем кратность его равна 4.
, причем кратность его равна 4.
2. Находим собственные векторы:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
|
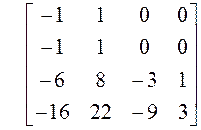
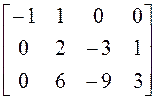 .
.
Общее решение системы:
![]() .
(15)
.
(15)
Число линейно независимых собственных векторов равно двум, значит, жорданова форма имеет две клетки.
3. Находим присоединенные векторы:
![]()
|
|
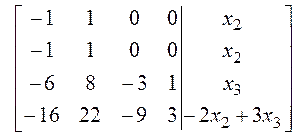
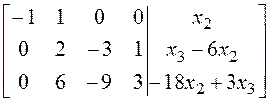 .
(16)
.
(16)
Система (16) имеет решения при любых значениях ![]() и
и ![]() ,
поэтому любой собственный вектор имеет присоединенный. Таким образом, обе
клетки имеют второй порядок, и жорданова форма выглядит так:
,
поэтому любой собственный вектор имеет присоединенный. Таким образом, обе
клетки имеют второй порядок, и жорданова форма выглядит так:
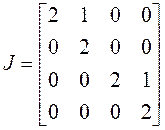 .
(17)
.
(17)
4. Матрица Т, приводящая А
к виду ![]() , – это матрица перехода от исходного
базиса к базису, в котором матрица оператора совпадает с
, – это матрица перехода от исходного
базиса к базису, в котором матрица оператора совпадает с ![]() . Из (4.65) видно, что
. Из (4.65) видно, что ![]() , т. е.
, т. е. ![]() и
и ![]() –
векторы собственные, а
–
векторы собственные, а ![]() и
и ![]() – присоединенные к ним. Чтобы
найти
– присоединенные к ним. Чтобы
найти ![]() и
и ![]() ,
записываем фундаментальную систему по решению (4.63):
,
записываем фундаментальную систему по решению (4.63): ![]() . Векторы
. Векторы ![]() и
и ![]() –
частные решения системы (16) при соответствующих значениях
–
частные решения системы (16) при соответствующих значениях ![]() и
и ![]() ,
т. е.
,
т. е. ![]() – решение системы
– решение системы
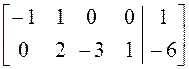 , а
, а ![]() – системы
– системы
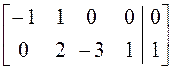 .
.
Например, ![]() . Таким
образом,
. Таким
образом,
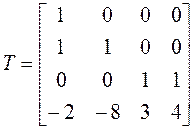 .◄
.◄
Пример 8.
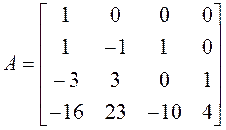 .
.
►Проведем вычисления по тому же плану, что и в первом примере.
![]()
![]()
![]() 1.
1.
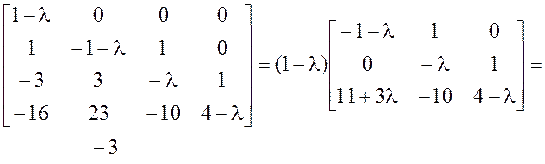
![]() .
.
Таким образом, ![]() .
.
2.
![]()
![]()
![]()
![]()
![]()
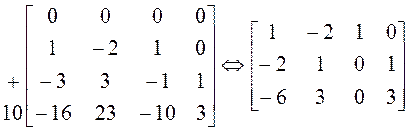 ;
;
![]() .
.
![]() , следовательно, число линейно независимых собственных
векторов равно двум, значит, матрице
, следовательно, число линейно независимых собственных
векторов равно двум, значит, матрице ![]() имеет две
клетки.
имеет две
клетки.
3.
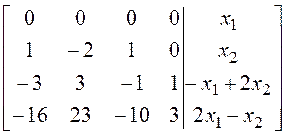 (18)
(18)
Система (18) имеет решение только в том случае, когда ![]() . Поэтому только один из
собственных векторов имеет присоединенные. Значит, одна из клеток будет иметь
первый порядок, а вторая – третий.
. Поэтому только один из
собственных векторов имеет присоединенные. Значит, одна из клеток будет иметь
первый порядок, а вторая – третий.
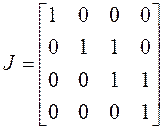 .
.
4.
![]() ;
; ![]()
![]() .
.
Находим ![]() и
и ![]() – присоединенные векторы к
– присоединенные векторы к ![]() :
:
![]()
![]()
![]()
![]()
![]()
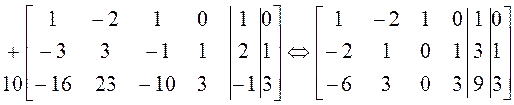 ,
,
![]() ;
;
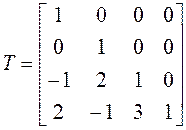 .◄
.◄
Задачи
24. Для
каждой из перечисленных матриц найти жорданову нормальную форму – матрицу ![]() и невырожденную матрицу
и невырожденную матрицу ![]() , приводящую заданную матрицу к
жордановой нормальной форме.
, приводящую заданную матрицу к
жордановой нормальной форме.
1)
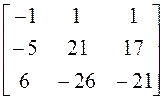 ; 2)
; 2) 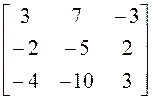 ;3)
;3) 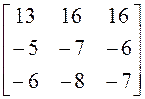 ;4)
;4) 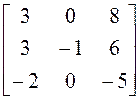 ;
;
5)
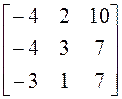 ; 6)
; 6) 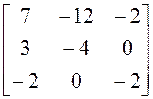 ; 7)
; 7) 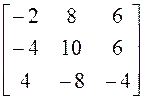 ; 8)
; 8) 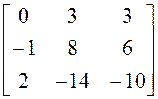 ;
;
9)
 ; 10)
; 10)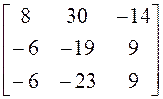 ; 11)
; 11)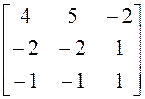 ; 12)
; 12) 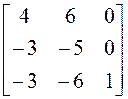 ;
;
13)
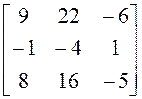 ; 14)
; 14)  ;15)
;15)  ; 16)
; 16)  ;
;
17) 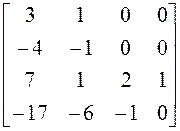 ; 18)
; 18) 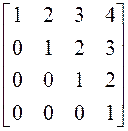 ; 19)
; 19) 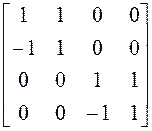 ;
;
20) 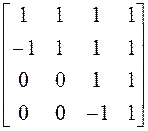 ; 21)
; 21)
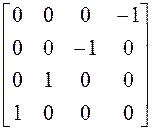 ; 22)
; 22) 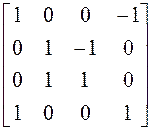 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.