Жорданова нормальная форма матрицы. Характеристический многочлен жордановой клетки, страница 2

Чтобы составить матрицу , опять находим собственные векторы. Однородная система с матрицей (14) имеет общее решение . Два линейно независимых собственных вектора с собственным значением  – это два ее линейно независимых частных решения (фундаментальная система решений):  и . Если же , то  

.

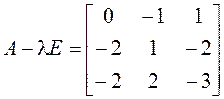Частное решение этой системы можно найти устно: . Таким образом, матрица , столбцами которой являются координатные столбцы соответствующих найденных векторов, имеет вид

.◄

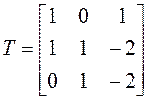Пример 4.

.

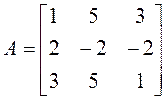►Составляем характеристический многочлен и находим его корни:

; .

Находим собственные векторы для двукратного корня с целью определения количества соответствующих ему клеток:

:   .

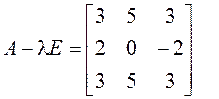Так как , то , т.е. этому собственному значению соответствует только один линейно независимый собственный вектора, значит, жорданова нормальная форма содержит одну клетку с этим собственным значением, имеющую второй порядок. Таким образом,

.

Если линейный оператор  в исходном базисе пространства имеет матрицу , а в базисе  – матрицу , то  (определяем по первому столбцу),  (по второму столбцу),  (по третьему). Таким образом, первый вектор искомого базиса – собственный с собственным значением , второй – присоединенный к нему, третий – опять же собственный, только с собственным значением . Находим эти векторы:

-3

:      ;

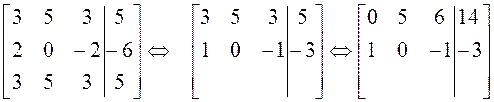Общее решение однородной системы , частное (собственный вектор) – . Чтобы найти  решаем неоднородную систему с той же матрицей, в которой столбцом свободных членов является координатный столбец вектора . Общее решение неоднородной системы , частное –  (присоединенный к ).

:      ; ;  .◄

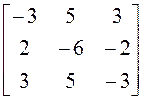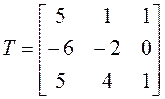Пример 5.

.

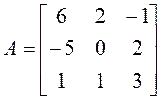►Как обычно, начинаем с характеристического многочлена:

;        .

, ,

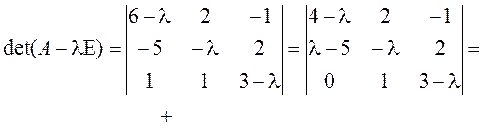
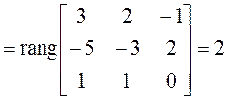значит, жорданова нормальная форма состоит из одной клетки третьего порядка:

.

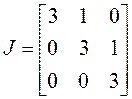Если линейный оператор  в базисе  имеет матрицу , то , , . Таким образом, первый вектор искомого базиса – собственный с найденным собственным значением, второй – первый присоединенный к нему, третий – второй присоединенный. Находим эти векторы:

-2

3

;

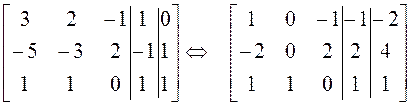Собственный вектор  (частное решение однородной системы), первый присоединенный  (частное решение неоднородной системы с первым столбцом свободных членов), второй присоединенный  (частное решение неоднородной системы со вторым столбцом свободных членов).

.◄

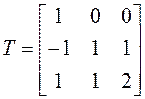Пример 6.

.

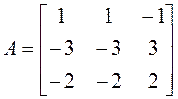►Характеристический многочлен:

;        .

, ,

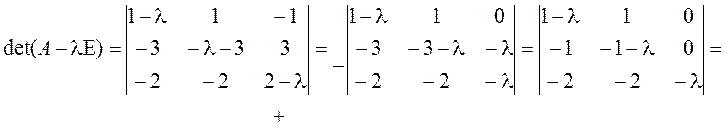
значит, жорданова нормальная форма имеет две клетки, одну второго порядка и одну первого:

.

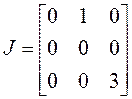По матрице  записываем: , , . Таким образом, первый вектор искомого базиса – собственный с найденным собственным значением , второй – присоединенный к нему, третий – опять же собственный. Сначала находим собственный вектор, решая однородную систему с матрицей . Ее общее решение . Если это решение выбрать в качестве столбца свободных членов, получим неоднородную систему