

































 Министерство образования Республики Беларусь
Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный технический университет имени П. О. Сухого»
Кафедра «Автоматизированный электропривод»
МОДЕЛИРОВАНИЕ ЭЛЕМЕНТОВ
И СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ ЭЛЕКТОРОПРИВОДАМИ
ЛАБОРАТОРНЫЙ ПРАКТИКУМ
подисциплине «Моделирование в электроприводах» для студентов специальности 1-53 01 05
«Автоматизированные электроприводы» дневной формы обучения
По дисциплине «Моделирование в электроприводах», согласно учебного плана, выполняются лабораторные работы.
Цель работ – закрепить полученные теоретические знания и научиться применять их для практических расчетов.
Отчет по лабораторным работам должен выполнятся на листах формата А4. Отчет должен содержать:
– титульный лист;
– цель работы;
– задание на лабораторную работу (структурная схема модели или система дифференциальных уравнений, числовые данные, указанные в задании);
– вывод системы уравнений в форме Коши, если в задании приведена структурная схема;
– расчет параметров модели;
– текст программы (кроме работ № 3 и 4);
– таблица с указанием имен и назначения всех переменных во всех подпрограммах программы (кроме работ № 3 и 4);
– распечатка документа MathCAD с диаграммами переходных процессов (для работы № 4 – распечатки диаграмм процессов, сделанные программой SMED); – выводы.
Моделирование – процесс изучения свойств объекта путем изучения свойств другого, более удобного для исследования объекта, находящегося в некоторой степени подобия с первым объектом. Математическая модель – система уравнений, описывающих взаимосвязь характеристик и параметров объекта и отражающая физические процессы, происходящие в объекте.
Математическое моделирование производится
путем численно![]() го
решения дифференциальных уравнений, которое заключается в расчете значений переменных
на текущем шаге Yi
по значениям переменных модели на других шагах расчета. Фактически производится
численное интегрирование функций, соответствующих правым частям дифференциальных
уравнений, записанных в форме Коши: ddytj =
f j (t,
X,Y);
го
решения дифференциальных уравнений, которое заключается в расчете значений переменных
на текущем шаге Yi
по значениям переменных модели на других шагах расчета. Фактически производится
численное интегрирование функций, соответствующих правым частям дифференциальных
уравнений, записанных в форме Коши: ddytj =
f j (t,
X,Y);
t y j (
)![]() ( )⋅dt .
( )⋅dt .
Математическое моделирование осуществляется в соответствии с одним из двух принципов:
1. По системе уравнений.
2. Структурное моделирование (моделирование по структурной схеме).
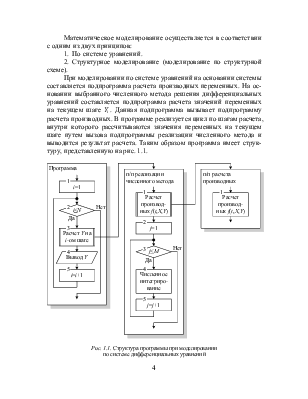
При моделировании по системе уравнений на основании системы составляется подпрограмма расчета производных переменных. На основании выбранного численного метода решения дифференциальных уравнений составляется подпрограмма расчета значений переменных на текущем шаге Yi . Данная подпрограмма вызывает подпрограмму расчета производных. В программе реализуется цикл по шагам расчета, внутри которого рассчитываются значения переменных на текущем шаге путем вызова подпрограммы реализации численного метода и выводится результат расчета. Таким образом программа имеет структуру, представленную на рис. 1.1.
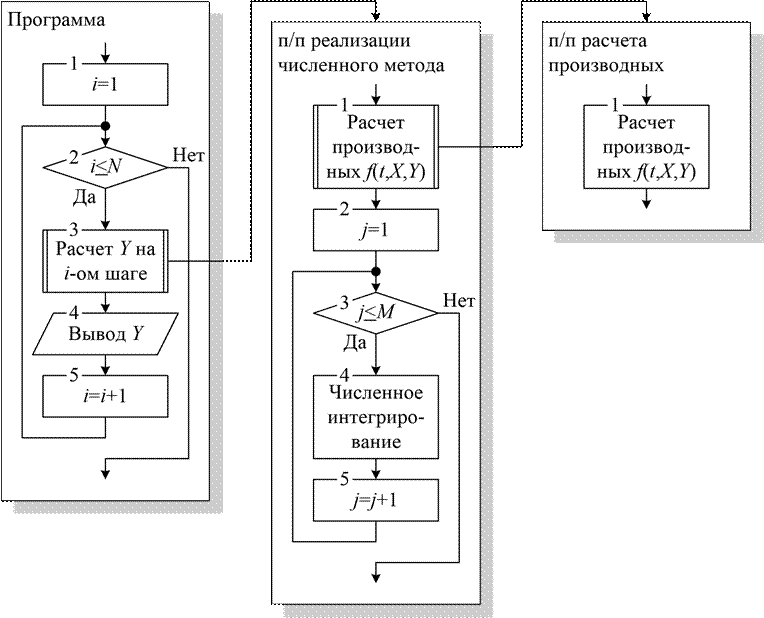
Рис. 1.1. Структура программы при моделировании по системе дифференциальных уравнений
При структурном моделировании для всех типов звеньев, входящих в состав модели, на основании выбранного численного метода и уравнения, описывающего звено, составляются подпрограммы для определения значения выходного сигнала звена. По структурной схеме модели составляется подпрограмма расчета значений переменных на текущем шаге Yi . Эта подпрограмма в порядке следования сигналов в модели вызывает подпрограммы звеньев. Сама программа выполняется аналогично моделированию по системе уравнений. Структура программы показана на рис. 1.2.
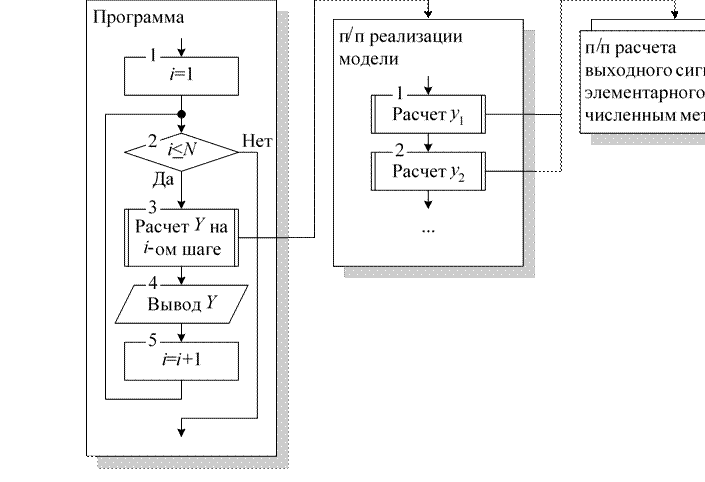
Рис. 1.2. Структура программы при структурном моделировании
Расчетные соотношения и параметры основных численных методов приведены в табл. 1.1. В расчетных соотношениях приняты обозначения:
Y – вектор переменных модели;
i – номер текущего шага расчета, для которого рассчитываются
значения переменных модели (соответствует моменту времени t);
∆t – шаг расчета (интервал времени между соседними шагами расчета); f – вектор значений правых частей дифференциальных уравнений, записанных в форме Коши; ν – номер текущей итерации.
Таким образом Yi – вектор значений переменных на текущем шаге расчета, т. е. в момент времени t = i⋅∆t, Yi−1 – на предыдущем шаге расчета (t − ∆t ) и т. д. Значения Yi−0,5 соответствуют времени посредине между текущим и предыдущим шагами расчета.
Некоторые методы имеют несколько итераций, номера которых записываются в верхнем индексе, т. е. значения переменных модели на текущем шаге рассчитываются несколько раз, постепенно уточняясь.
Таблица 1.1 Расчетные соотношения и параметры численных методов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.