Математическое моделирование. Структура программы при моделировании по системе дифференциальных уравнений, страница 3

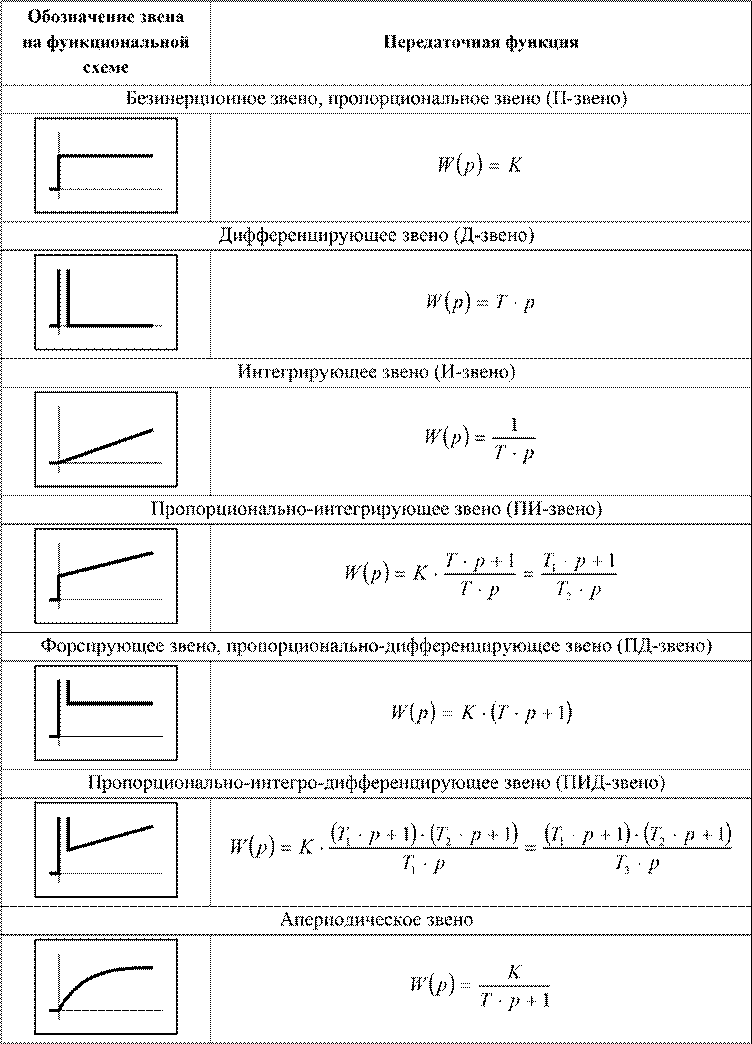
Таблица 1.3 Передаточные функции динамических звеньев

Оставим в левой части только p⋅ y(p), чтобы при переходе от операторной формы к функциям времени получить дифференциальное уравнение в нормальной форме Коши:

T ⋅ p⋅ y(p)= K ⋅ x(p)− y(p),  p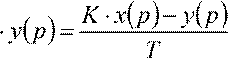,  dy ₌ K ⋅ x − y . dt        T

Для форсирующего получится алгебраическое уравнение с производной для входного сигнала звена

W( )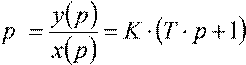     , y( )p = K ⋅(T ⋅ p +1)⋅ x(p),

y( )p = K ⋅T ⋅ p ⋅ x(p)+ K ⋅ x(p),

y = K ⋅T ⋅ ^dx + K ⋅ x.

dt

Если перед форсирующим звеном стоит апериодическое или интегрирующее, как показано на рис. 1.3, то в алгебраическое уравнение для форсирующего звена можно подставить выражение для производной его входного сигнала y из уравнения в форме Коши предыдущего звена.

 

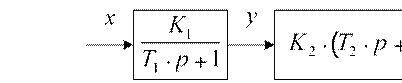
Рис. 1.3. Пример структурной схемы

                                                  ^y( )p = T _⋅^Kp1₊1⋅ x( )p ,   

1

^z( )p = K₂ ⋅(T₂ ⋅ p +1)⋅ y( )p ,

                                                             ddyt ₌ K₁ ⋅Tx1 − y ,        



z = K2 ⋅T2 ⋅ ddyt + y,

                                                   ^ddyt ₌ K₁ ⋅Tx1 − y ,        

z = K2 ⋅T2 ⋅ K1 _⋅Tx1 ₋ y ₊ y.

Если в правой части присутствует производная переменной, для которой в системе записано алгебраическое уравнение, или производная входного сигнала, то можно прибегнуть к численному дифференцированию, заменив производные на отношения:

                                   ∆        − ₋                                                                        ∆ ( )− ( − ∆ ⁾_.

1.5.  Модели двигателей постоянного тока  независимого и последовательного  возбуждения

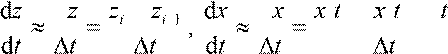При постоянстве магнитного потока (kΦ = kΦ_Н = const ) из полной модели двигателя можно исключить цепь возбуждения. При этом структурная схема модели примет вид, представленный на рис. 1.4.

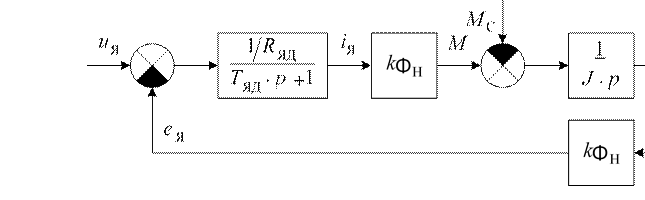
Рис. 1.4. Структурная схема модели ДПТ НВ:

u_Я – напряжение якоря; e_Я – ЭДС якоря; i_Я – ток якоря; M – момент двигателя; 

M_С – момент сопротивления; ω – угловая скорость вращения; R_ЯД – активное  сопротивление якорной цепи двигателя; T_ЯД – постоянная времени якорной цепи

= LЯД , где L_ЯД – индуктивность якорной цепи двигателя

T_ЯД

R_ЯД

Для двигателей последовательного возбуждения необходимо учитывать нелинейность кривой намагничивания. Структурная схема модели двигателя последовательного возбуждения при упрощенном представлении цепи возбуждения (без учета влияния вихревых токов) представлена на рис. 1.5.

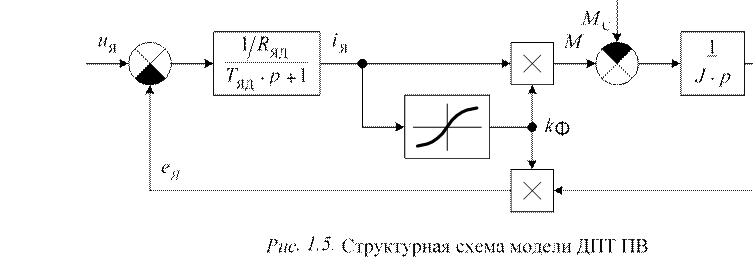
На схеме нелинейное звено от i_Я до kΦ моделирует кривую намагничивания. Кривую намагничивания для двигателей серии Д можно аппроксимировать кусочно-линейной функцией, представленной на рис. 1.6. По осям отложены относительные значения тока обмотки возбуждения и потока двигателя (отнесенные к номинальным значениям).

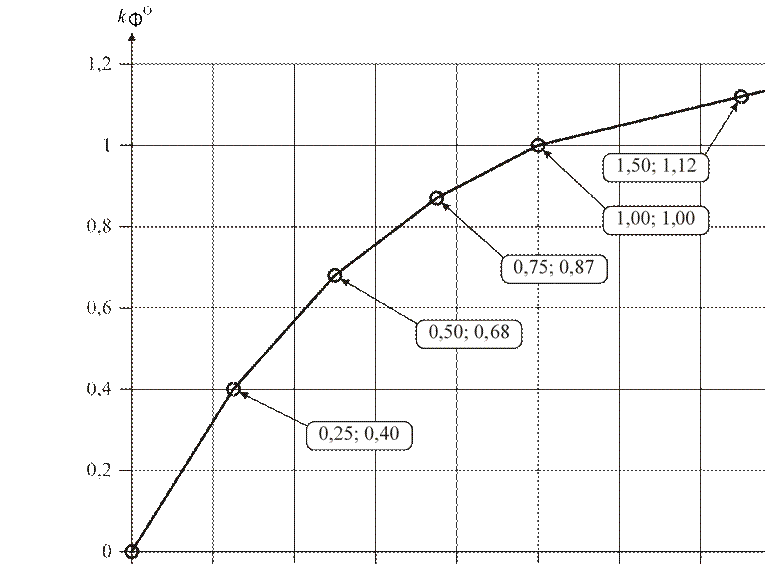
           0             0,2           0,4           0,6           0,8             1             1,2           1,4           1,6

Рис. 1.6. Аппроксимация кривой намагничивания двигателей серии Д

При определении параметров якорной цепи следует иметь ввиду, что для двигателя последовательного возбуждения в них необходимо включить параметры обмотки возбуждения.

Недостающие параметры двигателя можно рассчитать по формулам (1.1)…(1.8) [1] по каталожным данным, приведенным в [2] и [3].

1.6.  Модель асинхронного электродвигателя  с короткозамкнутым ротором

В зависимости от решаемой задачи модель асинхронного электродвигателя удобно представлять в одной из трех координатных систем: αβ, xy или dq.

В координатной системе αβ система уравнений (разрешенная относительно потокосцеплений), описывающая асинхронный электродвигатель имеет вид

^dψdt1α = u1α − L ⋅RL12⋅−L2L122 ⋅ψ1α + L1 ⋅RL12⋅−L12L122 ⋅ψ2α,

                                       1

                dψ1β = u1β − ⋅RL12⋅−L2L122 ⋅ψ1β + L1 ⋅RL12⋅−L12L122 ⋅ψ2β,

                    dt                L1

               dψ2α = −   R2 ⋅ L1  2 ⋅ψ2α + L1 ⋅RL22⋅−L12L122 ⋅ψ1α − ωЭЛ ⋅ψ2β,