Математическое моделирование. Структура программы при моделировании по системе дифференциальных уравнений, страница 7

3.1.  Моделирование по системе уравнений

Дана структурная схема, представленная на рис. 3.1. Обозначим переменные модели:

–  x – входные воздействия;

–  y – сигналы, для которых будут составлены дифференциальные уравнения в форме Коши (выходные звенья динамических звеньев, имеющих оператор Лапласа в знаменателе передаточной функции);

–  z – сигналы, для которых будут записаны алгебраические уравнения (выходные сигналы статических звеньев, а также динамических, не имеющих оператор Лапласа в знаменателе передаточной функции).

2

Рис. 3.1. Структурная схема

Составим систему уравнений.

Уравнение для вычитателя: z₁ = x₁ − y₁ .

Передаточная функция интегрирующего звена:

                                                                 W( )     .

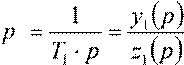Выразим операторное изображение выходного сигнала звена:

y.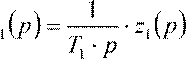

Умножив на оператор Лапласа, получим выражение для производной выходного сигнала звена в операторной форме:

p.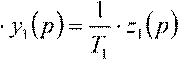

Перейдя к функциям времени получим дифференциальное уравнение в форме Коши:

ddyt1 = T¹₁ ⋅ z₁.

Передаточная функция апериодического звена:

                                                            W( )   .

Выразим операторное изображение выходного сигнала звена: y₂ ( )        .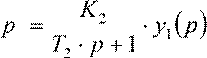

Умножим на знаменатель передаточной функции и раскроем

скобки в левой части уравнения:

y₂ ( )p ⋅(T₂ ⋅ p +1) = K₂ ⋅ y₁(p),

T₂ ⋅ p ⋅ y₂ (p)+ y₂ (p) = K₂ ⋅ y₁(p).

Перенеся второе слагаемое из левой части в правую и разделив на постоянную времени T₂ , получим выражение для производной выходного сигнала звена в операторной форме:

T₂ ⋅ p⋅ y₂ (p) = K₂ ⋅ y₁(p)− y₂ (p),

p.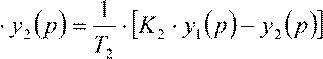

Перейдя к функциям времени, получим дифференциальное

уравнение в форме Коши:

                                                               ^d     .

Для выходного сигнала звена с ограничением запишем алгебраическое выражение по табл. 1.2 с учетом выбранных обозначений сигналов и параметров звеньев.

z₂ = K₃ ⋅ y₂,

z2 = Y−0Y3,03   ,при   при      z2z>2 <Y03−,Y03.

Таким образом получим систему уравнений:

z1 = x1 − y1,

ddyt1 = T11 ⋅ z₁,

                                                     ddyt2 = T1₂ ⋅(K2 ⋅ y1 − y2 ),    



z2 = K3 ⋅ y2,

z2 = Y−₀Y₃,03   ,при   при      z₂z>2 <Y₀₃−,Y03.



Составим подпрограмму расчета правых частей дифференциальных уравнений и алгебраических уравнений по составленной системе. При этом выделим в отдельную подпрограмму расчет значений входных воздействий. В рассматриваемом примере входное воздействие одно. Пусть вид входного воздействия – скачок

⁼ ^0,   при   t < 0≥,0. ^x1 x_m1,   при   t

В строках 3, 4 приведенного ниже фрагмента программы производится объявление типа переменной – одномерного массива. Без объявления типа передавать в подпрограммы переменные массивы нельзя. В строках 6…13 объявлены глобальные переменные программы. В строке 8 объявлены массивы для хранения параметров звеньев и входных воздействий (назначение остальных переменные рассмотрим позже):

lK – коэффициенты передачи звеньев; lT – постоянные времени звеньев; ly0 – уровни ограничения звеньев; xm – амплитуда входных воздействий.

В строках 15…19 находится подпрограмма расчета значений входных воздействий. Параметры подпрограммы: t – значение текущего времени; x – рассчитываемые значения входных воздействий.

В строках 21…32 находится подпрограмма, написанная по составленной системе уравнений. Параметры подпрограммы: Y, Z – массивы значений переменных; F – массив рассчитываемых значений правых частей дифференциальных уравнений (dydt )^; t – значение текущего времени. Внутренняя переменная x – значения входных воздействий.

01 Program Example;

02

03  Type

04  DArray = array [1..10]  double;of

05

06  Var

07  Y, Yp, Z,

08  lK, lT, ly0, xm: DArray;

09  tk, dt, t: double;10   i,

111312   f: text;   filename:    N: integer;string;                            x1 =_0x,m1  ,при  при  t  <t 0≥,0.