Математическое моделирование. Структура программы при моделировании по системе дифференциальных уравнений, страница 4

                     dt           L1 ⋅ L2 − L12

                 dψ2β = −    R2 ⋅ L1  2 ⋅ψ2β + L1 ⋅RL22⋅−L12L122 ⋅ψ1β + ωЭЛ ⋅ψ2α,

                    dt           L1 ⋅ L2 − L12

M = L ⋅pLД2⋅−L12L122 ⋅(ψ1β ⋅ψ2α − ψ1α ⋅ψ2β),

                           1

        dωdtЭЛ = pJД ⋅(M − MС),                                                     

где ^ψ₁α …^ψ₂β – потокосцепления обмоток; u₁α , u₁β – напряжения на обмотках статора; M , M_С – момент двигателя и момент сопротивления; ω_ЭЛ – угловая скорость вращения ротора: 

ω

                                                                                  ω_ЭЛ =      ;

p_Д

R₁, L₁ – активное сопротивление и индуктивность фазы обмотки статора; R₂, L₂ –активное сопротивление и индуктивность фазы обмотки ротора; L₁₂ – взаимоиндуктивность между обмотками статора и ротора; p_Д – число пар полюсов двигателя; J – момент инерции ротора двигателя.

При этом напряжение на обмотках статора

u₁α =U₁ ⋅  2 ⋅k_C ⋅cos(ω₀ЭЛ ⋅t), ^u₁β =U₁ ⋅   2 ⋅k_C ⋅sin(ω₀ЭЛ ⋅t),

где U₁ – действующее значение напряжения; k_C – коэффициент согласования при переходе от трех- к двухфазной модели

k_C =  ;

^ω₀ЭЛ – угловая скорость вращения векторов напряжения ω₀ЭЛ = 2⋅π⋅ f ;

f – частота напряжения.

В осях xy модель асинхронного двигателя выглядит следующим образом

dψdt1x = u1x − L1 ⋅RL12⋅−L2L122 ⋅ ψ1x + L1 ⋅RL12⋅ −L12L122 ⋅ ψ2x + ω0ЭЛ ⋅ ψ1y,

dψdt1y = u1y − L₁ ⋅RL12⋅−L2L122 ⋅ ψ1y + L1 ⋅RL12⋅ −L12L122 ⋅ ψ2y − ω0ЭЛ ⋅ ψ1x,

dψdt2x = − L R2 ⋅ L1 2 ⋅ ψ2x + L1 ⋅RL22⋅ −L12L122 ⋅ ψ1x + (ω0ЭЛ − ωЭЛ) ⋅ ψ2y, 1 ⋅ L2 − L12

^dψdt2y = − L₁ ⋅RL2 ⋅−L1L 2 ⋅ ψ2y + L1 ⋅RL22⋅ −L12L122 ⋅ ψ1y − (ω0ЭЛ − ωЭЛ) ⋅ ψ2x,

                                              2          12

M =      ⋅pLД2⋅−L12L12 ⋅ (ψ1y ⋅ ψ2x − ψ1x ⋅ ψ2y),

                     L1                        2



dωdtЭЛ = pJД ⋅ (M − MC).                                                               

Напряжения статора:

                                                                u1x ==U0.1 ⋅ 2 ⋅kC ,

u_1y

При записи модели в осях dq необходимо добавить уравнение для электрического угла поворота ротора ϕ_ЭЛ:

^dψdt1d = u1d − L ⋅RL12⋅−L2L122 ⋅ψ1d + L1 ⋅RL12⋅−L12L122 ⋅ψ2d + ωЭЛ ⋅ψ1q ,

                                   1

dψd1q = u1q − ⋅RL12⋅−L2L122 ⋅ψ1q + L1 ⋅RL12⋅−L12L122 ⋅ψ2q − ωЭЛ ⋅ψ1d , t      L1

dψdt2d = − L₁ R2 ⋅ L1 2 ⋅ψ2d + L1 ⋅RL22⋅−L12L122 ⋅ψ1d , ⋅ L2 − L12

      dψdt2q = − L₁ ⋅RL2₂⋅ L1L 2 ⋅ψ2q + L1 R 2⋅ L 122 1q ,

− 12

M = L ⋅pLД ⋅−L12L 2 ⋅(ψ1q ⋅ψ2d − ψ1d ⋅ψ2q ),

                       1       2          12

dωdtЭЛ = pJД ⋅(M − MC),

             dϕЭЛ = ωЭЛ.                                                                                   

 dt

Напряжения на обмотках статора при этом равны (при постоянстве ^ω₀ЭЛ):

                                          u_1d = U₁ ⋅  2 ⋅ k_C ⋅ cos(ω₀ЭЛ ⋅ t − ϕ_ЭЛ),

                                       ^u_1q = U₁ ⋅  2 ⋅ k_C ⋅ sin(ω₀ЭЛ ⋅ t − ϕ_ЭЛ).

Параметры модели асинхронного электродвигателя с короткозамкнутым ротором можно определить по формулам (2.1)…(2.5), (2.8)…(2.10) [1], по каталожным данным, приведенным в [4].

1.7.  Модели систем управления скоростью  двигателя постоянного тока  независимого возбуждения

На рис. 1.7 и 1.8 приведены структурные схемы одноконтурной и двухконтурной систем автоматического управления скоростью двигателя постоянного тока независимого возбуждения.

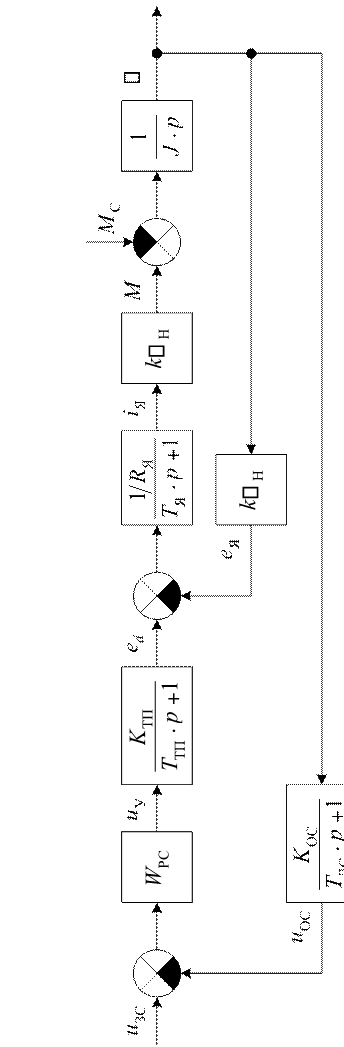
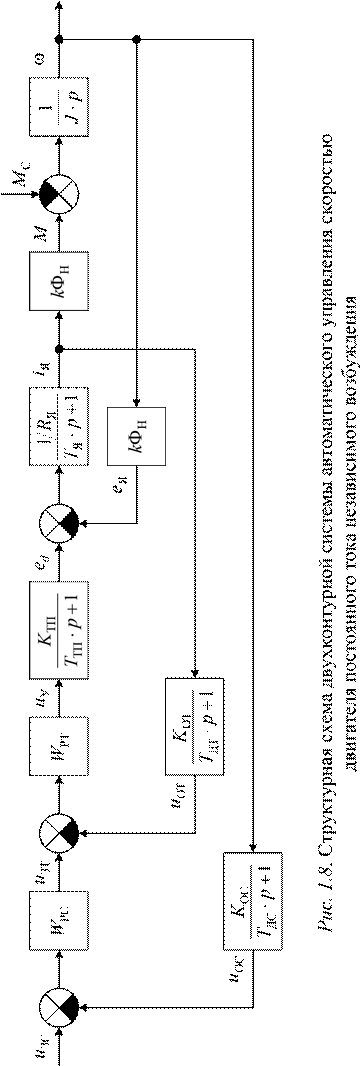
На схемах обозначено:

u_ЗС, u_ЗТ – напряжения задания скорости и тока; u_ОС, u_ОТ – напряжения обратных связей по скорости и току; u_У – напряжение управления тиристорным преобразователем; e_d – ЭДС тиристорного преобразователя;

W_РС, W_РТ – передаточные функции регуляторов скорости и тока;

K_ОС, K_ОТ – коэффициенты передачи обратных связей по скорости и току;

T_ДС, T_ДТ – постоянные времени датчиков скорости и тока;

K_ТП –           коэффициент передачи тиристорного преобразователя