Математическое моделирование. Структура программы при моделировании по системе дифференциальных уравнений, страница 9

В строке 93 закрывается файл вывода.

75  Begin

76  pIn;

77  assign(f, filename);

78  rewrite(f);

79  fillchar(Y, sizeof(Y), 0);

80  fillchar(Yp, sizeof(Yp), 0);

81  fillchar(Z, sizeof(Z), 0);

82  t := 0;

83  writeln(f,t:13:5,Y[1]:13:5,Y[2]:13:5,Z[2]:13:5);

84  N := round(tk/dt); 85   for i := 1 to N do 86     begin

87  t := dt*i;

88  cY(Yp, t, dt, Y, Z);

89  writeln(f, t:13:5, Y[1]:13:5, Y[2]:13:5,

90  Z[2]:13:5);

91  Yp := Y; 92     end;

93   close(f); 94 End.

На рис. 3.2 приведен документ MathCAD с построенными диаграммами переходных процессов.

3.2.  Структурное моделирование

При структурном моделировании нет необходимости делить переменные модели на те, для которых записаны дифференциальные уравнения, и те, для которых записаны алгебраические. Поэтому обозначим переменные, как показано на рис. 3.3.

Начальная часть программы с объявлениями переменных будет отличаться от предыдущего примера отсутствием массива Z, поскольку сейчас все переменные модели обозначены y.

Подпрограмма cX будет полностью такой же, как и в предыдущем примере.

a := READPRN("example.out")

〈 〉

Рис. 3.2. Документ MathCAD

 

Рис. 3.3. Структурная схема

001 Program Example;

002 

003 Type

004   DArray = array [1..10] of double;

005 

006 Var

007   Y, Yp,

008   lK, lT, ly0, xm: DArray;

009   tk, dt, t: double;

010   i,

011   N: integer;

012   f: text;

013   filename: string;

014 

015 Procedure cX(t: double; var x: DArray); 016 begin

017   if t >= 0 then x[1] := xm[1]

018   else x[1] := 0;

019 end;

020

Составим на основе метода Эйлера подпрограммы-функции расчета значения выходного сигнала звена на текущем шаге для всех типов звеньев, входящих в состав модели:

1. Вычитатель.

x  y         Вычитатель описывается выражением

y  = x₁ − x₂ .

021 Function Sub(X1, X2: double): double;

022 begin

023    :=  - ;Sub X1  X2 024 ;end

025                                       y=x₁ −x₂        

2. Интегрирующее звено.

  Выходной сигнал звена в операторной форме      y( )      .

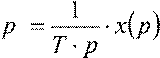Составим дифференциальное уравнение для выходного сигнала, аналогично рассматриваемым ранее примерам

 x.

Применив метод Эйлера к данному уравнению, получим y_i  x.

026 Function Int(X, Yp, T, dt: double): double;

027 begin

028    :=  + dt* /T;Int   Yp  X 029 ;end

030                                  i          i−1             T1        

3. Апериодическое звено.

  Выходной сигнал звена в операторной форме

                                                                                    y( )p = _{T ⋅}^K_{p +1}⋅ x( )p .

Составим дифференциальное уравнение для выходного сигнала

.

Применив метод Эйлера к данному уравнению, получим y_i .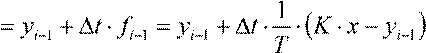

031 Function Ap(X, Yp, K, T, dt: double): double;

032 begin

033    :=  + dt*(K* - )/T;Ap   Yp  X Yp 034 ;end

035                         y_i

4. Звено с ограничением.

  Звено с ограничением описывается выражением

                                                                                   y = K ⋅ x,

y = Y−0Y,   0,при   при      y >y <Y0−,Y0.

036 Function Lim(X, K, y0: double): double; 037 var

043   Lim := y;

044 ;end

045

Теперь, по структурной схеме составим подпрограмму расчета значений всех переменных модели на текущем шаге.

046 Proce dure cY(Yp: DArray; t, dt: double;

047   var Y: DArray);

048 var

049   x: DArray; 050 begin

051   cX(t, x);

052   Y[1] := Sub(x[1], Y[2] ;)

053   Y[2] := Int(Y[1], Yp[2], lT[1], dt ;)

054   Y[3] := Ap(Y[2], Yp[3], lK[2], lT[2], dt); 055   Y[4] := Lim(Y[3], lK[3], ly0[3] ;)

005567  end;                                 

 

Рис. 3.4. Структурная схема

Подпрограмма ввода исходных данных будет точно такой же, как и в прошлом примере.