Классификация общепромышленных установок. Статические и динамические нагрузки электроприводов подъемных лебедок, страница 7

Значения результирующего коэффициента С_п для конвейеров на подшипниках качения.

Тип конвейера	Сп·10-2
Канатная дорога	0,6-0,7
Ленточные и цепные конвейеры	2,0-2,5

                                                                                                                                                                                                     

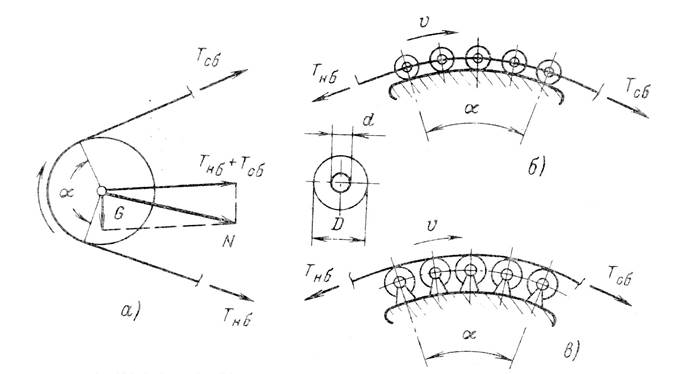
Рис. 7. Участки изгиба тягового элемента на блоке (а), шине (б) и батарее роликов (в).

На участках изгиба (рис. 7) сила сопротивления движению  ΔF_и состоит из двух слагаемых: силы от изгиба тягового элемента, пропорциональной натяжению в набегающей точке участка Т_нб и сила трения в подшипниках блоков или роликов, пропорциональной равнодействующей силе N на участке. Следовательно, 

ΔF_и = εT_нб + NμdD, (15) где ε– коэффициент сопротивления от изгиба тягового элемента.

В конвейерных установок обычно выполняются условия:

T_нб >> C_s (рис.7);

ΔF_и << T_нб.

Поэтому при определении равнодействующей N можно пренебречь весом блока C_s и принять, что натяжения в набегающей Т_нб и сбегающей Т_сб точках участка равны. Тогда выражение (15) приводится к виду:

ΔFи ≈ СиТнб,

                                                           d       d

              где  С_и = ε + 2μ    sin           – результирующий коэффициент сопро-

                                                           D       2

тивления на участке изгиба. Значения коэффициента С_и для различных конструктивных исполнений тягового элемента конвейера приведены в таблице 2.

Таблица 2.

Значения результирующего коэффициента сопротивления движению С_п на участках изгиба трассы конвейера.

Вид  участка изгиба трассы	№ рисунка	Угол обхва- та α	Сп·10-2
Звездочка с цепью и шкив с канатом	7,а	90-180о	2-3
Барабан с лентой	7,а	90-180о	4-6
Цепь с катками на шине	7,б	20-45о	1,2-3
Лента на роликовой батарее	7,б	20-45о	1,2-3
Цепь на роликовой батарее	7,в	30-60 о	2,5-3,7

Сила сопротивления вызывает увеличение натяжения тягового элемента на каждом участке.

Для прямолинейного участка:

Т_сб = Т_нб + ΔF_п , (17) для участка изгиба:

Т_сб = ^Т_нб + Δ^F_и = ^К_и^Т_нб, (18)                                                                                

гдеK_и =1+ С_и– коэффициент увеличения натяжения на данном участке.

 

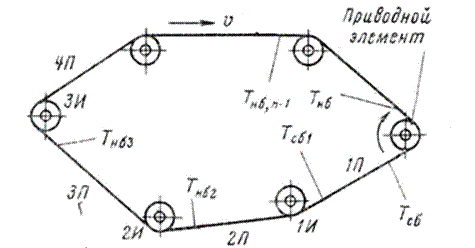
Рис. 8. Общая схема конвейерной линии.

В общем случае конвейер может состоять из многих участков (рис. 8). Поскольку прямолинейные участки отделяются друг от друга участками изгиба, то по всей замкнутой конвейерной линии имеется одинаковое число n  прямолинейных и криволинейных участков.

Таким образом, результирующая сила сопротивления движению определяется как сумма сил всех участков: 

                                n                  n                  n                                                     n

F_ст =∑ΔF_пi +∑ ∑ΔF_иi = q_il_i(C_п cosβ_i +sinβ_i )+∑C_иiT_нбi , (19)

                              i=1              i=1               i=1                                                 i=1

Так как силу F_cт должен преодолеть приводной элемент, то очевидно, что при установившемся движении разность натяжений на нем уравновешивается силой сопротивления:

Fст = Тнб −Tсб, (20)

Второе слагаемое в (19) зависит от натяжения, по этому для расчета F_cт необходимо последовательно определять натяжения на всех участках. При этом должно быть известно заранее натяжение в какой либо точке тягового органа, которое и принимается за исходную в расчете. Допустим, что нам известно место расположение приводного элемента и натяжение на его сбегающей точке. Следуя от этой точки по направлению движения тягового элемента, пронумеруем все прямолинейные участки П и участки изгиба И, как это показано на рис. 8. В соответствии с (19) и рис. 8, определив последовательно натяжения на входе участков изгиба, выразим T_нб на приводном элементе через исходно принятое значение Т_сб: