Классификация общепромышленных установок. Статические и динамические нагрузки электроприводов подъемных лебедок, страница 3

                  F₁ = C_s + C_{s o} + q_k x ± F ^' , (3)

                   F₂ = C_{s пр} + q_k (H − x)± F_тр^'' , (4) где C_s – вес поднимаемого груза.

С учетом (1) результирующее усилие равно:

                     F =С_s −αC_{s ном} + q_k (2x − H)±(F_тр^' + F_тр^'' ), (5) где знак плюс соответствует подъему кабины, а минус – спуску.

Результирующее усилие F удобно представить в виде алгебраической суммы активного усилия F_гр и реактивного, обусловленного трением усилия F_тр. Эти составляющие определят соответственно активную М_гр и реактивную М_тр составляющую приведенного к валу двигателя статического момента М_ст. Составляющая М_гр должна учитывать, кроме трения в направляющих, все потери на трение в подъемной лебедке.

Тогда имеем:

[Сs + qk(2x − H)−αCsном]Dкш

                   Mст =Мгр +Мтр =   + Mтр , (6)

2ip

где i_p – передаточное число редуктора

Из соотношения (6) следует, что статический момент зависит  от нагрузки кабины, от коэффициента уравновешивания α, от веса ветвей каната. При этом М_ст является функцией пути.

Если высота подъема невелика (до H =15 м) составляющая  q_k (2x − H)≈ 0. Тогда при подъеме номинального (C_s = C_sном) и пустой кабины М_стможно определить с помощью соотношений:

(1− α)Сs номDкш

                 Mст1 = Mгр + Mтр =  + Мтр, (7)

2i_pη_п.ном

− αСsномDкш

M_ст2 = −M_гр + M_тр =          η_{п. ном}, (8)                                                      2ip

где η_{п. ном} – К.П.Д. подъемной установки с учетом трения в направляющих, соответствующий номинальной нагрузке.

Находим статический момент при спуске:

                      '                                             (1− α)СsномDкш

                 Mст1 = Mгр − Mтр =  ηп. ном, (9)

2ip

                      '                                                 − αСsномDкш

                 M_ст2 = −M_гр − M_тр =  , (10)                                       

2i_pη_п. ном

Влияние коэффициента уравновешивания α на требуемую мощность можно оценить с помощью среднеквадратичного момента нагрузки М_ск, задавшись определенным циклом работы. Например, примем, что цикл состоит из подъема номинального груза и спуска пустой кабины.

Полагая t_п = t_c = t_р с помощью (9) и (10) получаем:

 M_ск =, (11)

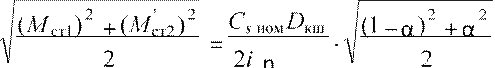p п. ном

Значение α=α_опт, при котором имеет место минимальное значение М_ск, можно определить, приравняв к нулю производную подкоренного выражения (11) d        ₂

(1− 2α + α ) = 0                       dα

αопт = 0,5

Оптимальное значение α зависит от параметров цикла работы и от потерь на трение в установке [2]. С учетом этого принимаемые при проектировании значения коэффициента уравновешивания лежат в пределах α = 0,4 ÷0,6.

При большой высоте подъема Н на статический момент в соответствии с (6) оказывает значительное влияние неуравновешенный вес подъемного каната. Этот вес изменяется в функции координаты х (см. рис. 2) и нарушает достигаемую выбором α=α_опт равномерность нагрузки. За счет этого требуемая мощность двигателя увеличивается. Поэтому при большой высоте подъема обычно прибегают к уравновешиванию веса подъемного каната с помощью уравновешивающего каната УК, показанного на рис. 2 штриховой линией. Для таких установок соотношения (7) – (10) применимы при любой высоте подъема.

Из (7) – (10) видно, что при α = 0,5 максимальные и минимальные нагрузки как по значению, так и характеру одинаковы при любом направлении движения (см. рис. 3)

 

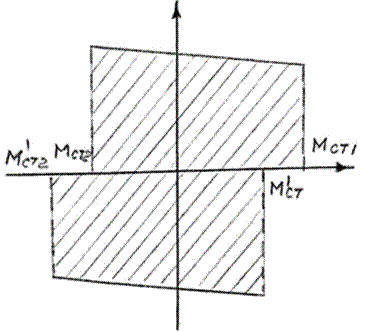
Рис. 3. Пределы изменения нагрузок электропривода двухконцевой лебедки

При проектировании двухконцевых подъемных лебедок используются симметрические схемы электропривода.

При расчете двухконцевых подъемных лебедок, в которых вместо противовеса используется второй подъемный сосуд (когда установка обслуживает только два уровня) можно пользоваться полученными соотношениями (7) – (10), полагая в них α = 0.

Динамические нагрузки двухконцевых подъемных установок определяются суммарным приведенным моментом инерции установки и допустимым ускорением в соответствии с выражением:

d

Mдин = J∑ ω= J∑εдоп, (12)