Предмет механики жидкости и газа. Параметры потока. Методы задания движения. Деформационное и вращательное движение жидкости

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

1.1. Предмет механики жидкости и газа

Гидромеханика, или механика жидкостей и газов, – наука о движении этих сред. Предметом изучения является модель сплошной текучей среды, под которой понимается непрерывное множество материальных точек или бесконечно малых объемов, способных заполнять собой окружающее пространство под действием приложенных сил.

1.2. Параметры потока

Сжимаемость. Способность среды оказывать сопротивление изменению объема под действием внешних сил давления называется сжимаемостью. Мерой сжимаемости является модуль объемного сжатия E

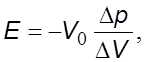                                                 (1.1)

где  – начальный объем,  – изменение давления,  – изменение объема.

Для жидкостей модуль объемного сжатия в десятки тысяч раз больше, чем для газов. Поэтому принято считать жидкости несжимаемыми  средами, а газы – сжимаемыми.

При движении газовых потоков со скоростями, составляющими менее 10% от скорости звука, их также можно считать несжимаемыми средами.

Плотность. Средняя плотность среды , есть отношение  где  – масса среды, находящаяся в объеме  Плотность в точке  В общем случае  Для однородной среды имеет место

Величина, обратная плотности , называется удельным объемом. Среды, для которых , называются баротропными.

Плотность газов зависит от давления  и температуры T. Для совершенных газов параметры связаны известным уравнением

                                                     (1.2)

или

                                                  (1.3)

В зависимости от изменения одного из параметров поток может быть изотермическим,  адиабатическим и изоэнтропическим.

При изотермическом течении

Адиабатический поток теплоизолирован от окружающей среды, и в этом случае

                                           (1.4)

где k – показатель адиабаты (или изоэнтропы – для потока идеального газа).

Изоэнтропический – это идеальный адиабатический поток, в котором отсутствует теплообмен с окружающей средой и не проявляются силы трения.

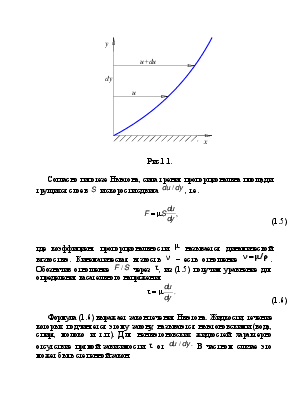
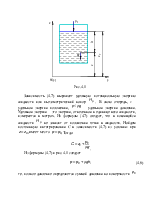
Вязкость. Способность среды оказывать сопротивление сдвигу называется вязкостью. При движении среды вдоль плоской поверхности скорость по нормали к поверхности изменяется от  при  до  при  (рис. 1.1.), где  – скорость на бесконечном удалении от поверхности.

Рис.1.1.

Согласно гипотезе Ньютона, сила трения пропорциональна площади трущихся слоев  и скорости сдвига , т.е.

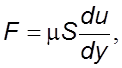                                                   (1.5)

где коэффициент пропорциональности  называется динамической вязкостью. Кинематическая вязкость  – есть отношение . Обозначив отношение  через , из (1.5) получим уравнение для определения касательного напряжения

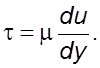                                                     (1.6)

Формула (1.6) выражает закон течения Ньютона. Жидкости, течение которых подчиняется этому закону, называются ньютоновскими (вода, спирт, молоко и т.п.). Для неньютоновских жидкостей характерно отсутствие прямой зависимости  от  В частном слкчае это может быть степенной закон

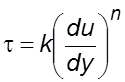.                                                  (1.7)

При  (1.7) преобразуется в закон (1.6).

В случае  жидкости называются псевдопластичными, при  – дилатантными. К первым относятся многие пищевые жидкости (кефир, сметана, тесто, фарш и т.п.), ко вторым – некоторые суспензии, краски и т.п. Существует множество других сред, законы течения которых отличаются от уравнения (1.7). Наука, изучающая движение неньютоновских жидкостей, называется реологией.

Вязкость несжимаемых жидкостей зависит от температуры, сжимаемых – и от давления. С увеличением температуры вязкость жидкостей снижается, а газов – увеличивается.

В теоретической гидрогазодинамике вводится понятие идеальной жидкости, у которой .

2. КИНЕМАТИКА ЖИДКОСТИ

2.1. Методы задания движения

Скорость или движение жидкости могут быть заданы двумя методами – Лагранжа и Эйлера.

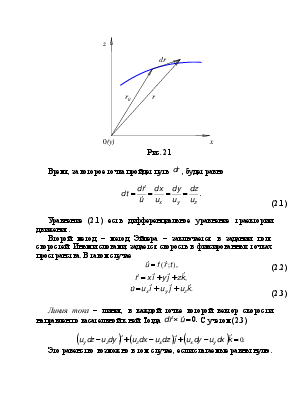
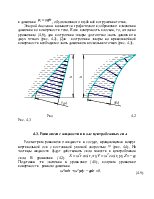
Метод Лагранжа заключается в задании траектории движения частиц жидкости.

Траектория – линия, по которой частицы жидкости перемещаются в пространстве (рис. 2.1). Траектория задается уравнением  скорость в данной точке  

В проекциях на координатные оси

.

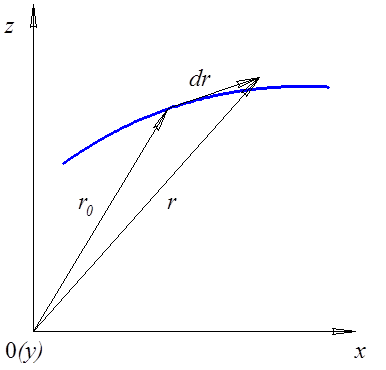
Рис. 2.1

Время, за которое точка пройдет путь , будет равно

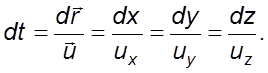                                       (2.1)

Уравнение (2.1) есть дифференциальное уравнение траектории движения.

Второй метод – метод Эйлера – заключается в задании поля скоростей. Иными словами, задается скорость в фиксированных точках пространства. В таком случае

                                                    (2.2)

                                           (2.3)

Линия тока – линия, в каждой точке которой вектор скорости направлен по касательной к ней. Тогда  С учетом (2.3)

Это равенство возможно в том случае, если слагаемые равны нулю. Следовательно,

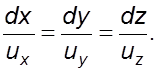                                                (2.4)

Вид уравнений (2.1) и (2.4) одинаков. Однако решение их различно.

Ускорение Из уравнения (2.2) следует

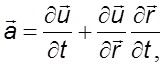
или