Одномерное течение отличается изменением параметров потока только в одном направлении. Уравнения этих течений являются частными случаями общих уравнений движения.
Уравнение неразрывности
![]() (5.8)
(5.8)
Уравнение переноса импульса. Из
уравнения (5.2) для установившегося одномерного потока при ![]() следует
следует
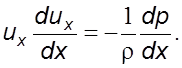 (5.9)
(5.9)
Интегрируя
это выражение, получим ![]() В итоге пришли к уравнению
Бернулли (5.7).
В итоге пришли к уравнению
Бернулли (5.7).
Уравнение энергии. Для изоэнтропийного потока уравнения переноса импульса и энергии тождественны.
В уравнении (5.7) первое слагаемое есть удельная энтальпия
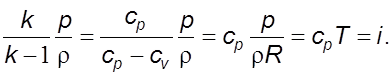 (5.10)
(5.10)
Таким образом, с учетом (5.10) уравнение (5.7) примет вид
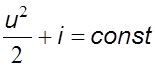 (5.11)
(5.11)
Постоянную
найдем из условия полного торможения потока, т.е. при ![]() :
:
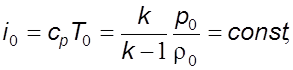 (5.12)
(5.12)
где ![]() –
удельная энтальпия заторможенного потока;
–
удельная энтальпия заторможенного потока; ![]() называются параметрами
заторможенного потока. При полном торможении вся кинетическая энергия потока
переходит в теплоту.
называются параметрами
заторможенного потока. При полном торможении вся кинетическая энергия потока
переходит в теплоту.
Из уравнения (5.11) с учетом (5.12) следует
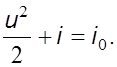 (5.13)
(5.13)
Часто используются и другие формы записи уравнения (5.13)
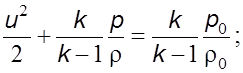 (5.13а)
(5.13а)
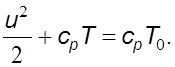 (5.13б)
(5.13б)
5.2.1. Скорость звука
Скорость
звука – это скорость распространения малых возмущений в данной среде. С целью
вывода зависимости для ее расчета обратимся к основам теории ударных волн.
Предположим, что в сечении 1 – 1 канала возникла сильная волна сжатия,
которая за время ![]() переместится
на расстояние
переместится
на расстояние ![]() в
сечение 2 – 2 (рис. 5.1). Скорость движения волны составляет
в
сечение 2 – 2 (рис. 5.1). Скорость движения волны составляет ![]() приращение
давления
приращение
давления ![]() а
приращение плотности
а
приращение плотности ![]() Под действием перепада
давления
Под действием перепада
давления ![]() за
счет изменения плотности
за
счет изменения плотности ![]() внутрь объема
внутрь объема ![]() втекает
масса газа
втекает
масса газа ![]() где
где ![]() –
живое сечение канала. С другой стороны, из уравнения неразрывности потока
следует
–
живое сечение канала. С другой стороны, из уравнения неразрывности потока
следует ![]() Из
двух последних выражений имеем
Из
двух последних выражений имеем
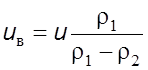 . (5.14)
. (5.14)
Зависимость (5.14) определяет взаимосвязь скорости распространения волны и скорости газа, движущегося позади фронта волны в том же направлении.
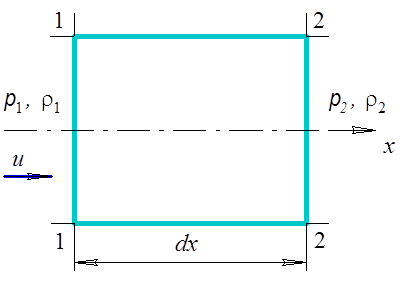
Рис. 5.1
Теперь
воспользуемся законом изменения количества движения для газа в объеме ![]() :
изменение количества движения равно импульсу силы, вызванной разностью давлений
в сечениях 1 – 1 и 2 –2,
:
изменение количества движения равно импульсу силы, вызванной разностью давлений
в сечениях 1 – 1 и 2 –2,
![]()
Отсюда скорость волны
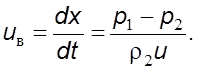 (5.14а)
(5.14а)
Решая данное уравнение совместно с зависимостью (5.14), получаем
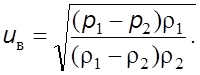 (5.15)
(5.15)
В
случае слабой волны ![]() и тогда
и тогда
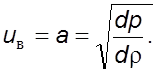 (5.16)
(5.16)
Слабая
волна является не чем иным, как акустической волной, поэтому формула (5.16)
определяет скорость звука ![]() . Из
сопоставления уравнений (5.15) и (5.16) следует, что скорость распространения
сильной волны сжатия всегда больше скорости звука.
. Из
сопоставления уравнений (5.15) и (5.16) следует, что скорость распространения
сильной волны сжатия всегда больше скорости звука.
Считая распространение звуковых волн изоэнтропийным, из уравнений (1.4) и (5.16) имеем
![]() (5.17)
(5.17)
5.2.2. Относительные параметры течения.
Газодинамические финкции
Из
уравнения (5.13) следует, что скорость достигает максимального значения при ![]() , и
тогда
, и
тогда ![]() .
Подставив сюда
.
Подставив сюда ![]() из
формулы (5.12), получим
из
формулы (5.12), получим
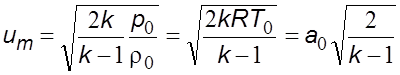 , (5.18)
, (5.18)
где
![]() –
скорость звука в заторможенном потоке,
–
скорость звука в заторможенном потоке,
![]() .
.
С учетом зависимостей (5.17) и (5.18) уравнение (5.13) можно записать в виде
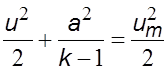 . (5.20)
. (5.20)
Из
уравнения (5.20) следует, что с увеличением ![]() до
до ![]() скорость
звука
скорость
звука ![]() изменяется
от
изменяется
от ![]() до
нуля (рис. 5.2). Точка А называется критической. Скорость в этой точке
называется критической
до
нуля (рис. 5.2). Точка А называется критической. Скорость в этой точке
называется критической ![]() и равна критической скорости
звука. Сечение канала, в котором скорость достигает значения
и равна критической скорости
звука. Сечение канала, в котором скорость достигает значения ![]() ,
называется критическим
,
называется критическим ![]() . В нем соответствующие
значения принимают все параметры потока (
. В нем соответствующие
значения принимают все параметры потока (![]() ;
; ![]() ;
; ![]() ).
).
Для критического сечения, согласно уравнениям (5.18) и (5.20), можно записать
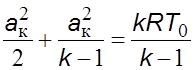 ,
или
,
или 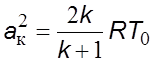 . (5.21)
. (5.21)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.