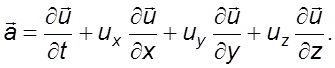 (2.5)
(2.5)
Первое слагаемое из уравнения (2.5) называется локальным ускорением и характеризует изменение скорости в данной точке пространства, сумма трех последних – конвективным. Оно обусловлено перемещением точки в пространстве.
Для
установившегося движения ![]()
2.2. Деформационное и вращательное движение жидкости
Линейная
деформация.
Рассмотрим движение элемента жидкости в виде отрезка 0А вдоль оси ![]() (рис.
2.2). Пусть за время
(рис.
2.2). Пусть за время ![]() точка переместится из
положения A в положение
точка переместится из
положения A в положение ![]() При этом приращение длины
отрезка составит
При этом приращение длины
отрезка составит ![]()
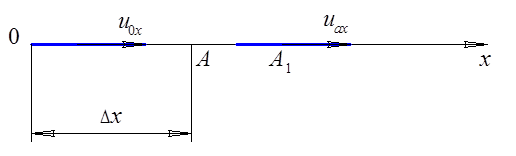
Рис. 2.2
Для
бесконечно малого отрезка ![]() имеем
имеем  и тогда
и тогда 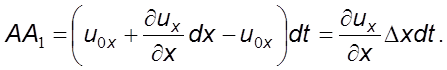 Скорость
относительного удлинения отрезка
Скорость
относительного удлинения отрезка ![]() , или скорость относительной
линейной деформации вдоль оси
, или скорость относительной
линейной деформации вдоль оси ![]() равна
равна
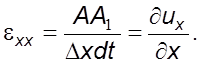
Аналогично для остальных осей
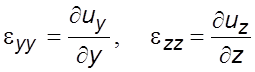 (2.6)
(2.6)
Таким образом, частные производные от составляющих скорости по одноименным координатам есть скорости относительных линейных деформаций элемента жидкости вдоль координатных осей.
Угловая
деформация.
Деформация может происходить по всем координатам. Выделим в жидкости элемент в
виде отрезка длиной ![]() ,
ориентированного вдоль оси 0
,
ориентированного вдоль оси 0![]() (рис. 2.3) в плоскости
(рис. 2.3) в плоскости ![]() 0
0![]() . За
время
. За
время ![]() он из
положения
он из
положения ![]() переместится
в положение
переместится
в положение ![]() . При
этом происходят его угловая и линейная деформации
. При
этом происходят его угловая и линейная деформации ![]()
d
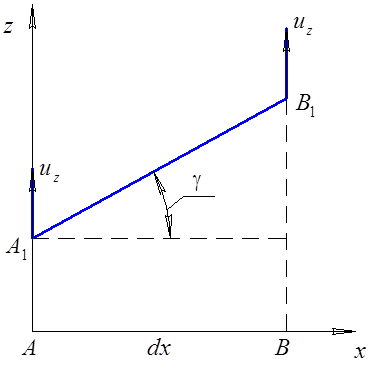
Рис. 2.3
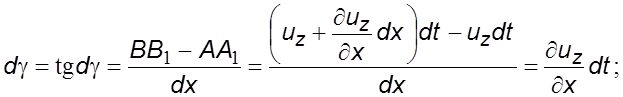 (2.7)
(2.7)
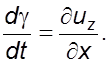 (2.7a)
(2.7a)
Аналогичным
образом можно получить следующие скорости угловых деформаций в плоскостях ![]() и
и ![]() :
:
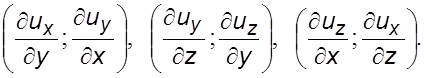 (2.8)
(2.8)
Таким образом, производные от составляющих скоростей по разноименным координатам есть скорости относительных угловых деформаций элемента жидкости, или его угловые скорости вращения относительно осей координат.
Из
выражения (2.8) видно, что первые две производные – это угловые скорости
вращения бесконечно малого отрезка относительно оси 0![]() , вторые –
относительно оси 0
, вторые –
относительно оси 0![]() и третьи – относительно оси 0
и третьи – относительно оси 0![]() .
.
Вихревое
движение жидкости. При движении жидкости можно наблюдать
образование вихрей (например, при встрече с препятствиями). Рассмотрим движение
элемента жидкости, имеющего проекцию на плоскость ![]() в виде
прямоугольника 0ABC. За время
в виде
прямоугольника 0ABC. За время ![]() прямоугольник повернется и
деформируется таким образом, что точка A переместится в положение
прямоугольник повернется и
деформируется таким образом, что точка A переместится в положение ![]() ,
, ![]() в
положение
в
положение ![]() и
т.д. (рис. 2.4). Согласно уравнению (2.7) и рис. 2.4,
и
т.д. (рис. 2.4). Согласно уравнению (2.7) и рис. 2.4,
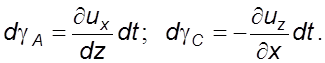
Средний угол поворота
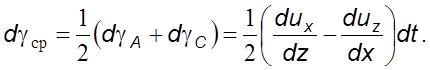
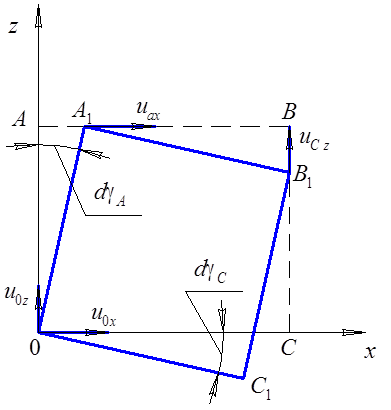
Рис. 2.4
Тогда
угловая скорость вращения элемента жидкости относительно оси 0![]()
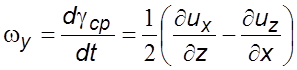 . (2.9)
. (2.9)
Аналогичным
образом можно записать величины ![]() и
и ![]()
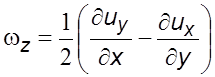 ;
;
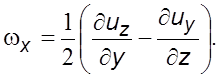
Выражение
в скобках обозначается (rot ![]() . Так как
. Так как ![]() то
то
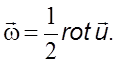 (2.10)
(2.10)
Для
безвихревого движения rot ![]()
Вихревая
линия –
линия, в каждой точке которой вектор угловой скорости ![]() направлен по
касательной к ней. В этом случае
направлен по
касательной к ней. В этом случае ![]() , из этого следует уравнение
вихревой линии
, из этого следует уравнение
вихревой линии
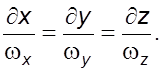 (2.11)
(2.11)
Трубка тока, элементарная струйка. Поверхность, образованная линиями тока, проведенными через точки произвольного контура, называется трубкой тока. Трубка тока бесконечно малого сечения, заполненная линиями тока, называется элементарной струйкой. Сечение, нормальное к линиям тока, называется "живым" сечением. Скорость по сечению элементарной струйки ввиду малости ее живого сечения постоянна и равна локальной скорости.
За
интервал времени ![]() через
живое сечение элементарной струйки (рис. 2.5) проходит объем жидкости
через
живое сечение элементарной струйки (рис. 2.5) проходит объем жидкости ![]() , где
, где ![]() и
и ![]() .
Величина элементарного объемного расхода
.
Величина элементарного объемного расхода ![]() , определяется в виде
, определяется в виде ![]() и,
следовательно,
и,
следовательно,
![]() (2.12)
(2.12)
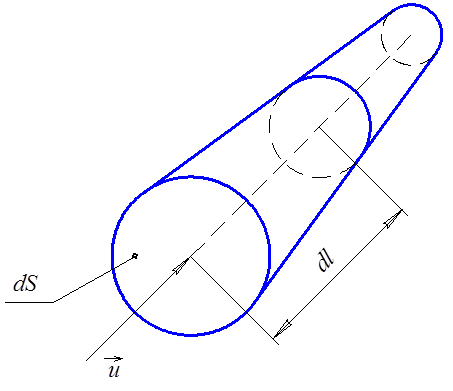
Рис. 2.5
Тогда
объемный расход жидкости ![]() через живое сечение потока
составит
через живое сечение потока
составит
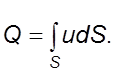 (2.13)
(2.13)
Средняя скорость потока равна
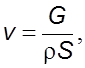 (2.14)
(2.14)
где ![]() –
массовый расход, кг/с, который связан с объемным расходом следующим образом:
–
массовый расход, кг/с, который связан с объемным расходом следующим образом: ![]()
Для несжимаемой жидкости
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.