Предмет механики жидкости и газа. Параметры потока. Методы задания движения. Деформационное и вращательное движение жидкости, страница 8

Таким образом,  и  и  определяются параметрами торможения. Из уравнений (5.20) и (5.21) после несложных преобразований можно получить

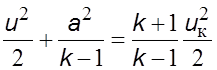.                                        (5.22)

Разделив обе части равенства (5.22) на , запишем

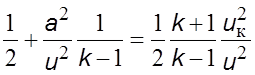.                                     (5.23)

Величина  (критерий Маха) характеризует отношение кинетической энергии к потенциальной энергии;  – отношение кинетической к полной энергии (приведенная скорость). С учетом безразмерных параметров М и  уравнение (5.23) можно представить в виде

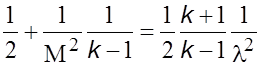.                                     (5.24)

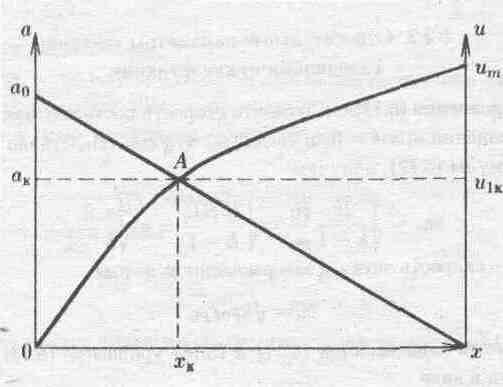
Рис. 5.2

Изменение М и  находится в пределах ; . При М < 1 поток считается дозвуковым, при М = 1 – звуковым и при М > 1 – сверхзвуковым. Газ можно считать несжимаемой средой, если , а при М > 0,1 обычно следует учитывать его сжимаемость (см. также указание в разд. 1.2).

После несложных преобразований уравнение (5.24) примет вид

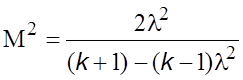.                                      (5.25)

Выразим теперь в относительных величинах значения . Разделив выражение (5.13б) на  и помня, что , с учетом уравнения (5.17) получим

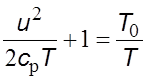,                                              (5.26)

или

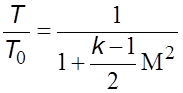.                                         (5.26а)

Из уравнений (1.2) и (1.4) следует

;   .

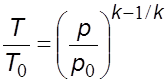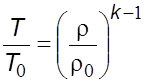Подставив эти значения  в формулу (5.26а), запишем

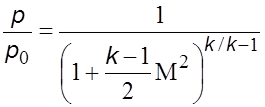,                                  (5.26б)

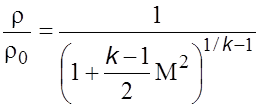.                                   (5.26в)

Таким образом можно установить связь между относительными параметрами и приведенной скоростью

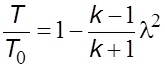,                                             (5.27)

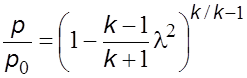,                                    (5.27а)

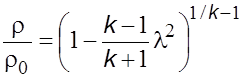.                                    (5.27б)

При  течение будет звуковое, и параметры имеют критические значения. В этом случае соотношения (5.27) имеют вид

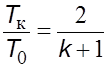,                                                 (5.28)

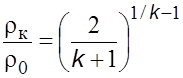,                                         (5.28а)

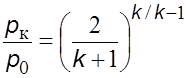.                                         (5.28б)

Приведенный удельный расход. Удельным расходом (плотностью потока) называется отношение массового расхода  к площади сечения потока

.                                                      

Выразим его через критические параметры полного торможения с учетом (5.27б)

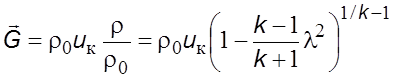.                          (5.29)

При  параметры имеют критические значения. Отношение  называется удельным приведенным расходом,

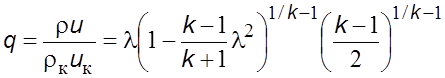.                     (5.30)

Газодинамическая функция  связывает геометрические параметры канала с основными параметрами потока.

В расчетах часто используется газодинамическая функция , равная отношению кинетической энергии к давлению полного торможения

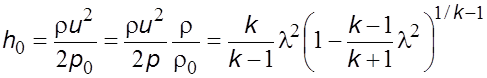.                  (5.31)

По уравнениям (5.26), (5.27), (5.30), (5.31) можно рассчитать любой параметр потока при известных других. Для облегчения расчетов эти функции сведены в таблицы газодинамических функций, которые приведены в литературе [1].

5.2.3. Движение газов в канале с переменной площадью

живого сечения

Продифференцировав выражение (5.8) по х, запишем уравнение (5.8) в следующем виде:

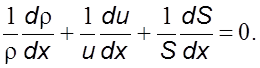                                     (5.32)

Так как для изоэнтропного процесса в баротропной среде  то

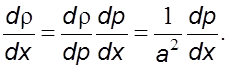                                        (5.33)

Из уравнений (5.32) и (5.33) следует

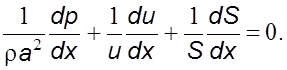
Подставив  из уравнения (5.9) и выполнив немногочисленные преобразования, получим

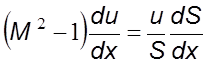                                          (5.34)

Уравнение (5.34) позволяет провести качественный анализ изменения параметра движения в канале с переменным сечением (таблица).

Отметим основные результаты такого анализа.

Дозвуковое движение (при М < 1):

– сечение убывает, скорость растет;

– сечение растет, скорость убывает.

Такая закономерность движения наблюдается в трубах, руслах, каналах.

В сверхзвуковом потоке (при М > 1):

– в диффузоре сечение увеличивается, то же происходит и со скоростью;

– в конфузоре сечение уменьшается, скорость падает.