Предмет механики жидкости и газа. Параметры потока. Методы задания движения. Деформационное и вращательное движение жидкости, страница 9

Таким образом, закономерности движения при  и  совершенно различны. Из формулы (5.34) видно, что в канале переменного сечения достичь скорости звука  можно только при экстремальном значении  При  это сделать невозможно, так как сечению  предшествует расширяющийся участок, в котором при М < 1 скорость падает, при М > 1 скорость возрастает.

Число Маха М	Производная скорости	Изменение сечения

Из формулы (5.34) следует также, что  может иметь экстремальное значение при  Это значит, что  и  при .

Сопло Лаваля. Труба, состоящая из конфузорной и диффузорной частей, называется соплом Лаваля (рис. 5.3). Она рассчитывается таким образом, что дозвуковая скорость на входе становится сверхзвуковой на выходе. Самое узкое сечение называется критическим. Соответствующие критические значения в нем имеют давление, плотность и температура.

u

Рис. 5.3

Расчет сопла Лаваля можно провести по уравнениям (5.26), разделив их на параметры потока в критическом состоянии (уравнение 5.28). В итоге получим

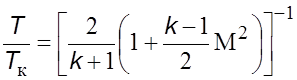,                                  (5.35)

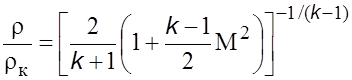,                           (5.35а)

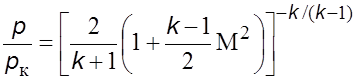.                          (5.35б)

Площадь поперечного сечения определяем из уравнения неразрывности (5.8)

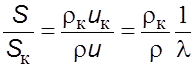.                                          (5.36)

Из уравнений (5.25), (5.35а) и (5.36) следует

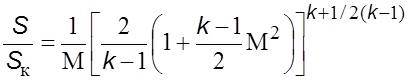.                        (5.37)

Согласно уравнению (5.37), данному значению  соответствует два значения М: одно для М < 1, другое для М > 1, при М = 1 имеет место .

Уравнения (5.35) и (3.37) соответствуют движению идеального газа. Влияние вязкости будет показано в разд. 6.

5.2.4. Прямой скачок уплотнения. Ударная адиабата

В сверхзвуковых потоках при снижении скорости могут возникать разрывы, называемые скачками уплотнения или ударными волнами.

В местах разрыва скорость снижается, а давление, температура и плотность резко (скачками) возрастает (рис. 5.4). Определим изменение параметров потока газа при скачке уплотнения. Запишем уравнение количества движения в виде . Так как, согласно уравнению (5.8), при  имеет место , то из предыдущей формулы следует . Это уравнение можно привести в виду

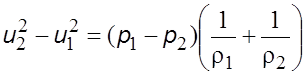.                                 (5.38)

Из уравнения (5.7) следует

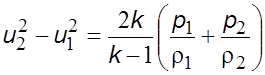.                                    (5.39)

Совместное решение уравнений (5.39) и (5.38) даст

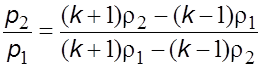.                                    (5.40)

Зависимость (5.40) называется уравнением ударной адиабаты.

Уравнение(5.40) можно выразить через безразмерные скорости. Учитывая, что , запишем

.

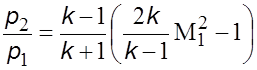Решив уравнения (5.38) и (5.39) относительно , найдем

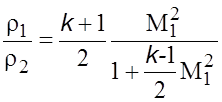.                                        (5.41)

Заменив отношение  отношением , из уравнений (1.2) и (5.41) найдем

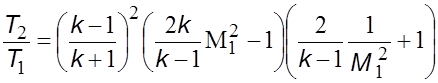.                      (5.42)

Уравнения (5.40), (5.41) и (5.42) описывают изменение параметров потока в прямом скачке уплотнения.

  Скачок

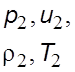
Рис. 5.4

5.3. Плоские потенциальные течения несжимаемой жидкости

Из плоских потенциальных течений представляет интерес вопрос силового взаимодействия рабочих колес гидромашин (турбин, центробежных компрессоров, вентиляторов и насосов) при обтекании их потоком идеального газа или жидкости.

Рассмотрим профиль, в виде цилиндра, и область, на которую распространяется возмущение этого профиля, обтекаемого потоком жидкости. Обозначим длину образующей цилиндра через , площадь боковой поверхности цилиндра , скорость набегающего потока  (рис. 5.5).

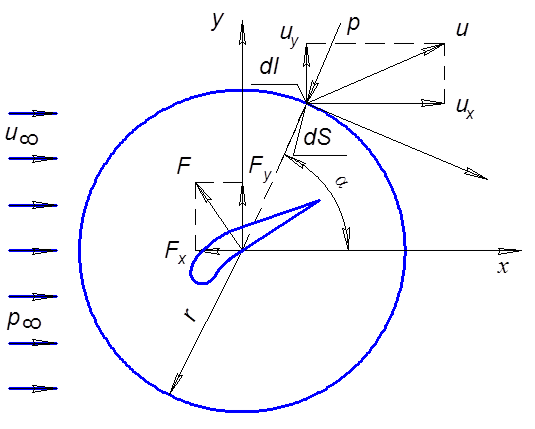
Рис. 5.5

Для решения задачи используем теорему об изменении количества движения. Изменение количества движения массы жидкости за единицу времени равно сумме всех внешних сил, действующих на эту массу. Теорема применяется к контрольной поверхности . Выделим на поверхности  площадку  где  – ширина цилиндра. На эту площадку воздействует сила давления  Проекция ее на оси координат равны  и  На профиль действует сила  ее проекции на оси  соответственно равны  и . Проекции равнодействующей силы на оси координат составляют