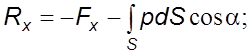Предмет механики жидкости и газа. Параметры потока. Методы задания движения. Деформационное и вращательное движение жидкости, страница 10

                                      (5.43)

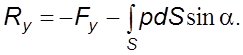                                     (5.43а)

Действие этих сил приводит к изменению количества движения массы жидкости, проходящей через контрольную поверхность за единицу времени  где  – объемный расход жидкости через контрольную поверхность. Проекции изменения количества движения на координатные оси равны

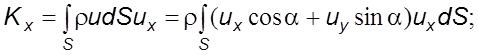                   (5.44)

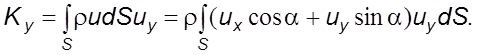                   (5.45)

Так как  а , то

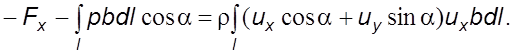
Из уравнений (5.43–5.44) с учетом

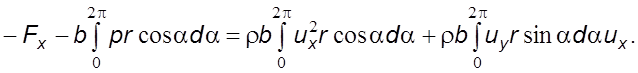
При увеличении радиуса от  до , при котором поток не испытывает возмущения от профиля,  получим

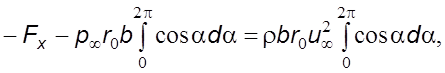
но 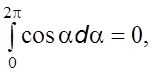 тогда , то есть сила лобового сопротивления равна нулю, так как отсутствуют силы трения.

Определим теперь силу . Из уравнений (5.43а) и (5.45) получаем .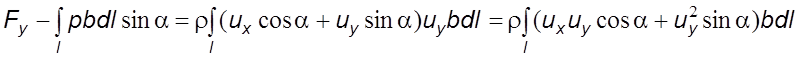

Так как  то

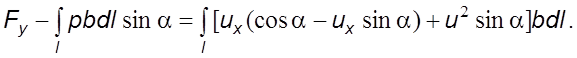           (5.46)

В уравнении (5.46) величина  С учетом этого равенства имеем

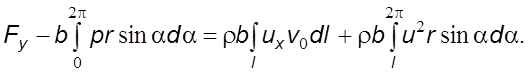               (5.47)

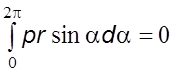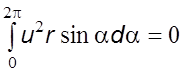В уравнении (5.47)  и  при  С учетом этих условий 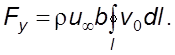 Так как  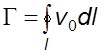– циркуляция скорости, то . Разделив обе части на , получим

                                                     (5.48)

Равенство (5.48) носит название теоремы Н.Е. Жуковского.

Вектор скорости , повернутый на  в сторону, противоположную направлению циркуляции, указывает направление действия подъемной силы.

Если вектор скорости совпадает с направлением оси 0, циркуляция направлена по часовой стрелке (Г<0), тогда  – положительная.

5.3.1. Обтекание решетки профилей

Лопатки рабочих колес турбин, центробежных насосов и компрессоров образуют решетки профилей. Для простоты рассмотрим прямолинейную решетку (рис. 5.6), для которой  – шаг решетки,  – хорда профиля,  – относительный шаг.

Параметры потока перед решеткой обозначим индексом 1, за решеткой – 2. Введем фиктивную скорость

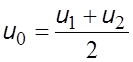.                                                   (5.49)

Согласно закону сохранения массы (это видно и из плана скоростей, показанного на рис. 5.6), .

Из закона сохранения энергии следует

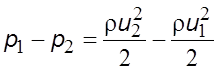.                                            (5.50)

Закон сохранения импульса для замкнутого контура АВСD дает

,

                                                 (5.51)

Так как  и , то из (5.50) следует

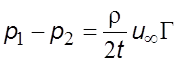,                                               (5.52)

где Г  – циркуляция скорости по контуру АВСD.

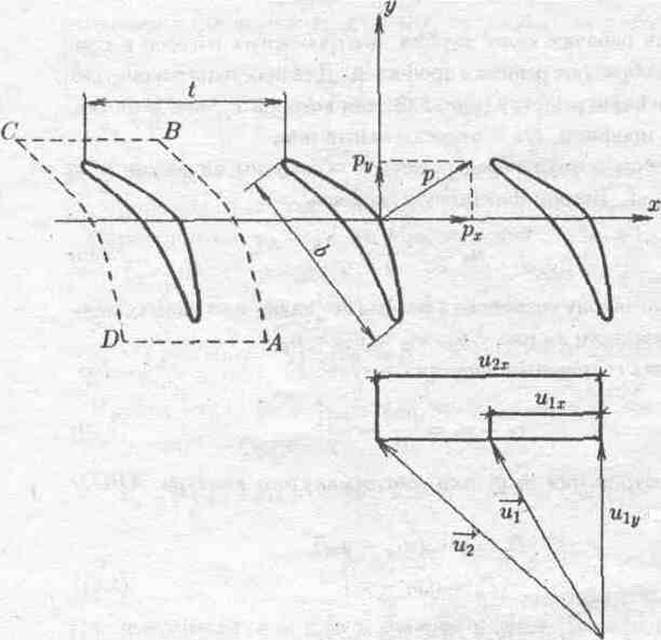
Рис. 5.6

Из уравнений (5.51) и (5.52) получим

,

.                                                  (5.53)

Поскольку , то

.                                                     (5.54)

Таким образом, в насосах и компрессорах лопатки колес будут оказывать силовое воздействие на жидкость или газ с силой . В турбинах поток будет вращать колесо, воздействуя на лопатки с такой же силой, создавая на выходном валу необходимый крутящий момент.

6. ДИНАМИКА ВЯЗКОЙ ЖИДКОСТИ

6.1. Режимы течения

Различают два режима течения – ламинарный и турбулентный. Ламинарное (слоистое) течение отличается постоянством во времени скорости и давления в любой точке потока. Такое течение существует при сравнительно небольшой скорости движения жидкости. При достижении некоторого критического значения скорости  происходит переход от ламинарного к турбулентному движению, которое характеризуется непрерывным изменением во времени скорости и давления в любой точке. Возникает пульсация этих параметров, в результате чего происходит интенсивное перемешивание жидкости по всему объему потока. Исследованиями было установлено, что критическая скорость, соответствующая переходу от одного режима к другому, зависит от вязкости, диаметра трубопровода. Количественно переход от одного режима к другому определяется величиной критерия Рейнольдса: . На практике наиболее часто принято считать, что при в трубопроводах имеет место ламинарный режим течения, при Re > 2300 – турбулентный.

Течение вязкой жидкости в общем виде описывается уравнением (3.21), несжимаемой – уравнением (3.23).

При решении задач гидродинамики турбулентных потоков вводится понятие осредненной составляющей скорости  и напряжения . Тогда их локальные значения будут равны