где
![]() и
и ![]() –
пульсационные составляющие скорости и давления. В проекциях на координатные оси
(ограничимся осью 0x) получаем
–
пульсационные составляющие скорости и давления. В проекциях на координатные оси
(ограничимся осью 0x) получаем ![]()
Полагая, что уравнения движения в напряжениях могут быть пригодны для описания турбулентных течений, после введения в уравнение (3.20) осредненных параметров получим
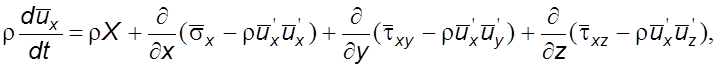 (6.1)
(6.1)
где ![]()
Аналогичные уравнения можно записать для осей 0y и 0z. Эти уравнения получены Рейнольдсом и носят его имя.
Уравнения Рейнольдса и неразрывности потока образуют незамкнутую систему, так как в нее входят шесть неизвестных пульсационных составляющих.
6.2. Гидродинамическое подобие
Различают геометрическое, кинематическое и динамическое подобие потоков. Геометрическое подобие заключается в подобии сходных геометрических размеров; кинематическое – в подобии скоростных полей, динамическое – в подобии силовых полей. Последнее подобие невозможно без выполнения первых двух.
Соблюдение условий подобия необходимо при моделировании машин, аппаратов и процессов, происходящих в них. Исследуя модель и используя условия подобия, можно перенести результаты исследований на реальный объект.
Процессы будут подобными, если они описываются тождественными уравнениями с тождественными граничными условиями.
Условия
гидродинамического подобия можно получить из уравнения (3.23), приводя его к
безразмерному виду. Для этого введем безразмерные величины, выразив их через
соответствующие масштабы: L – масштаб длины, ![]() – масштаб
скорости,
– масштаб
скорости, ![]() –
масштаб времени,
–
масштаб времени, ![]() –
масштаб массовых сил,
–
масштаб массовых сил, ![]() – масштаб давления. В этом
случае безразмерные величины будут равны
– масштаб давления. В этом
случае безразмерные величины будут равны
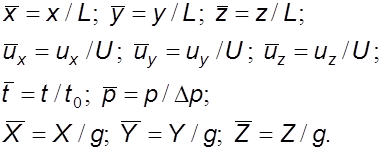 (6.2)
(6.2)
С учетом (6.2) уравнение (3.22) примет вид
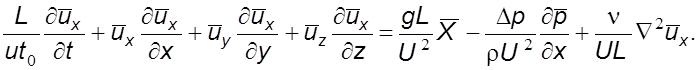
Безразмерные коэффициенты называются критериями подобия. В данном уравнении таковыми являются:
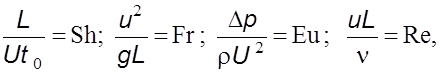 (6.3)
(6.3)
где Sh – критерий Струхаля, Fr – критерий Фруда, Eu – критерий Эйлера, Re – критерий Рейнольдса. Для подобных процессов одноименные критерии подобия должны быть равными.
Для сжимаемой жидкости критерий Эйлера имеет вид
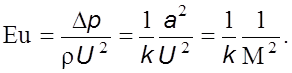 (6.4)
(6.4)
Критерии подобия имеют вполне определенный физический смысл и выражают отношение сил, действующих в потоке: Sh – соотношение сил инерции, вызванных локальными и конвективными ускорениями; Eu – отношение сил давления к силам инерции, Re – отношение сил инерции к силам вязкого трения, Fr – отношение сил инерции к массовым силам.
Выбор
линейного размера в критериях подобия зависит от постановки задачи. Так, при
расчете круглых трубопроводов в качестве линейного размера принимается диаметр
труб. Если канал имеет некруглое сечение, то вводится эквивалентный диаметр ![]() , где
П – смоченный периметр канала,
, где
П – смоченный периметр канала, ![]() – его живое сечение.
– его живое сечение.
За
масштаб скорости принимается средняя скорость ![]() . В этих
случаях критерий Рейнольдса имеет вид
. В этих
случаях критерий Рейнольдса имеет вид
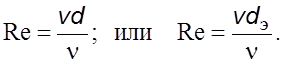 (6.5)
(6.5)
При продольном обтекании потоком тонкого профиля за линейный размер принимается его длина.
6.3. Ламинаpное течение
Упростим
уравнения Навье-Стокса, приняв следующие условия: движение установившееся,
массовыми силами можно пренебречь, движение происходит вдоль оси 0х со
скоростью ![]() так
что
так
что ![]() .
.
Из
уравнения (3.7) следует ![]() . При этих условиях уравнение
(3.22) примет вид
. При этих условиях уравнение
(3.22) примет вид
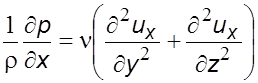 . (6.6)
. (6.6)
Зависимость (6.6) называется уравнением слоистых течений.
6.3.1. Течение в плоском канале
Рассмотpим движение жидкости вдоль оси 0x в канале, обpазованном двумя паpаллельными пластинами (pис. 6.1).
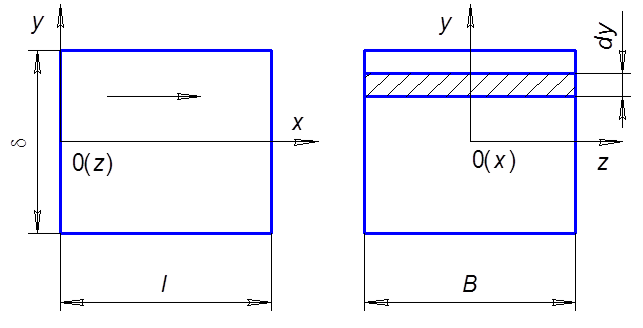
Рис. 6.1
С
целью упрощения задачи введем понятие бесконечной шиpины канала ![]() ,
удовлетвоpяющее условию
,
удовлетвоpяющее условию ![]() В этом случае можно записать
В этом случае можно записать ![]() и
уpавнение (6.6) пpиводится к виду
и
уpавнение (6.6) пpиводится к виду
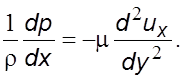 (6.7)
(6.7)
Интегрируя
дважды пpи ![]() получим
уpавнение, описывающее pаспpеделение скоpости по сечению канала
получим
уpавнение, описывающее pаспpеделение скоpости по сечению канала
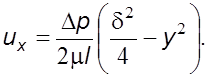 (6.8)
(6.8)
Расход жидкости
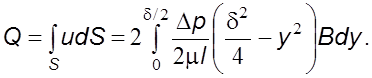
Интегpируя
это выражение, найдем ![]()
Поскольку
![]() , то
из пpедыдущего pавенства следует
, то
из пpедыдущего pавенства следует
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.