Предмет механики жидкости и газа. Параметры потока. Методы задания движения. Деформационное и вращательное движение жидкости, страница 3

Поверхность, образованная вихревыми линиями, называется вихpевой трубкой (рис. 2.6). Для вихревой трубки справедливо равенство  Из этого равенства следует, что сечение вихревой трубки не может быть равным нулю, так как  не может равняться бесконечности.

Циркуляция скорости. Циркуляцией скорости Г по контуру на участке AB (рис. 2.7) называется криволинейный интеграл

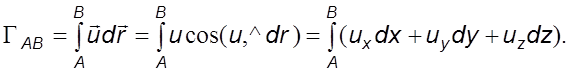
Циркуляция по замкнутому контуру равна

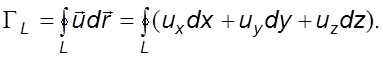                           (2.15)

               

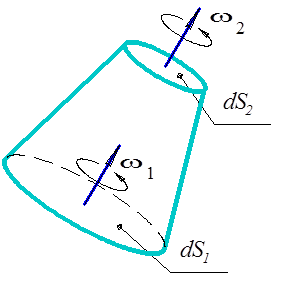
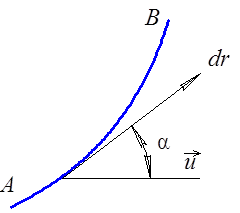
Рис. 2.6                                             Рис. 2.7

3. ОСНОВНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ

СПЛОШНОЙ СРЕДЫ

3.1. Уравнение неразрывности

Это уравнение выражает закон сохранения массы для движущейся сплошной среды. Выделим в пространстве произвольный объем жидкости  c поверхностью  (рис. 3.1.)

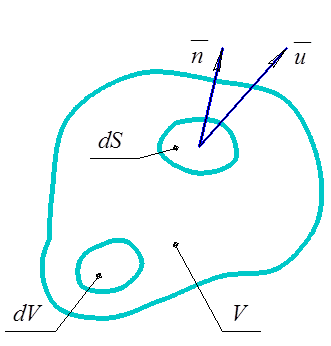
Рис. 3.1

Масса жидкости в объеме составляет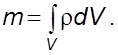

Изменение массы во времени равно

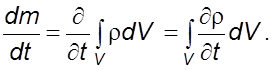                                      (3.1)

Это изменение возможно только за счет притока жидкости через площадь поверхности S:

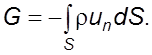                                                (3.2)

Значения массового расхода в уравнениях (3.1) и (3.2) равны, поэтому

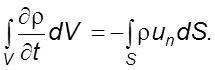                                           (3.3)

Преобразуя поверхностный интеграл в объемный, получим

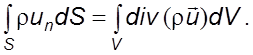                                        (3.4)

Подставив (3.4) в (3.3) и просуммировав подынтегральные функции, получим

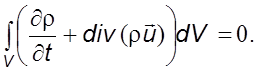
Поскольку объем  произволен и пределы интегрирования не ограничены, можно приравнять к нулю подынтегральную функцию. В результате получим уравнение неразрывности в дифференциальной форме

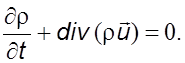                                              (3.5)

Для несжимаемой жидкости , и уравнение (3.5) примет вид

                                                     (3.6)

или в проекциях на координатные оси

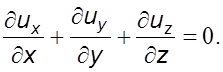                                          (3.7)

3.2. Силы, действующие в жидкости

Силы делят на внутренние и внешние. Внутренними называются силы взаимодействия между частицами жидкости (молекулами). Внешние силы приложены к жидкости извне. Последние делятся на массовые и поверхностные. К массовым силам относятся сила тяжести, инерционные силы, к поверхностным – силы давления и трения.

Массовые силы пропорциональны массе жидкости и равны произведению массы на плотность распределения этой силы:

                                                    (3.8) где

По существу, плотность распределения массовых сил  есть ускорение этих сил.

Через проекции на координатные оси вектор  может быть представлен в виде

                                             (3.9)

Поверхностные силы пропорциональны площади поверхности, на которую они действуют. Напряжение сил на площадке с нормалью n к ней определяется равенством

                                         (3.10)

В общем случае напряжение  зависит от координат x; y; z, времени t и ориентации площадки в пространстве. Если площадка зафиксирована, то  можно разложить по координатным осям.

Рассмотрим для примера площадку, перпендикулярную оси 0x (рис. 3.2).

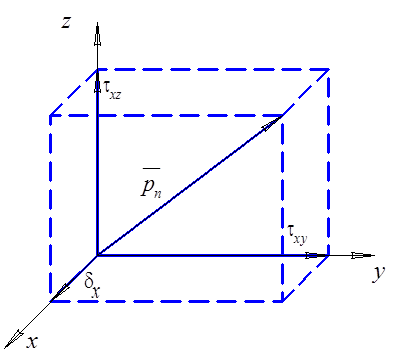
Рис. 3.2

В общем случае вектор  может не совпадать с направлением нормали, и его можно разложить на соответствующие компоненты, т.е. Аналогичным образом можно записать для площадки, нормальной к остальным осям,

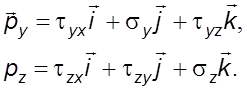                                      (3.11)

При произвольном расположении площадки с внешней нормалью n вектор  может быть представлен в виде равенства

или в проекциях на координатные оси

             (3.12)

Таким образом, вектор напряжения  определяется девятью скалярными величинами  и может быть выражен тензором напряжений

                                                         

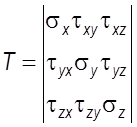
Так как тензор симметричен относительно главной диагонали, то  и  Таким образом, напряжение определяется только шестью скалярными величинами. В покоящейся жидкости, согласно уpавнению (1.6), касательные напряжения равны нулю. Тогда из уравнений (3.12) следует, что   но  есть проекции  на соответствующие оси, т.е. , а давление в точке, равное , не зависит от ориентации площадки в пространстве.