
















1.1 Общий алгоритм моделирования процесса ТТ
В данной работе предлагается алгоритм моделирования процесса стружкообразования [[i]], целью которого является аналитическое определение сил резания и распределения контактных напряжений на поверхностях лезвия при заданных режимах и условиях обработки, геометрии и свойствах материалов системы «инструмент-заготовка» .
Учитывая особенности процесса ТТ, принимаем следующую упрощенную физическую модель процесса при прямоугольном резании. Внедрение лезвия в материал заготовки с заданной скоростью приводит к возникновению напряженно-деформированного состояния (НДС) материала заготовки, подчиняющегося законам теории пластичности. При этом считаем, что материал заготовки является упруго-пластической средой с линейным упрочнением (см. раздел 3 и рисунок 3.4). В результате относительного движения стружки по передней поверхности и заготовки вдоль задней поверхности лезвия имеет место трение, приводящее совместно с процессами деформирования к выделению тепла, которое в свою очередь , перераспределяясь, вызывает изменение свойств среды, и, следовательно, влияет на НДС и процесс образования новой поверхности. Таким образом, получаем замкнутую систему (систему резания), в которой происходящие процессы взаимно обуславливают характер протекания каждого из них и влияют друг на друга.
Принимая во внимание взаимосвязь и взаимовлияние описанных выше процессов в виде принятого математического описания, приходим к алгоритму, представляющего собой итерационный процесс расчета сил резания и свойств упрочненного и нагретого материала в конечном числе точек цикла обработки с учетом результатов расчета в предыдущих точках. В этих точках вычислительная процедура сводится к численному интегрированию системы дифференциальных уравнений теории пластичности (см. раздел 3). Как указывалось ранее, в настоящее время для решения подобных задач широко используют конечноразностные (КР) методы и метод конечных элементов (КЭ), что не исключает возможности применения и других методов.
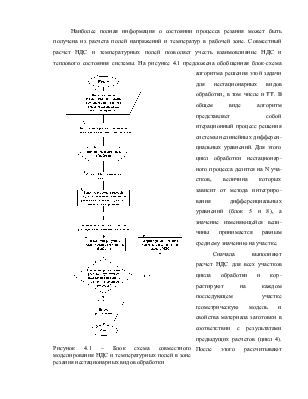
Наиболее полная информация о состоянии процесса резания может быть получена из расчета полей напряжений и температур в рабочей зоне. Совместный расчет НДС и температурных полей позволяет учесть взаимовлияние НДС и теплового состояния системы. На рисунке 4.1 предложена обобщенная блок-схема алгоритма решения этой задачи для нестационарных видов обработки, в том числе и ТТ. В общем виде алгоритм представляет собой итерационный процесс решения системы нелинейных дифференциальных уравнений. Для этого цикл обработки нестационарного процесса делится на N участков, величина которых зависит от метода интегрирования дифференциальных уравнений (блок 5 и 8), а значение изменяющейся величины принимается равным среднему значению на участке.
|
Рисунок 4.1 – Блок схема совместного моделирования НДС и температурных полей в зоне резания нестационарных видов обработки |
Сначала выполняют расчет НДС для всех участков цикла обработки и корректируют на каждом последующем участке геометрическую модель и свойства материала заготовки в соответствии с результатами предыдущих расчетов (цикл 4). После этого рассчитывают интенсивность и закон распределения источников и стоков теплоты (блок 7) и выполняют расчет температурных полей в зоне резания в течение всего цикла “резание» (блок 8).
Итерационный процесс прекращается в случае изменения контролируемой величины (например, максимальной температуры резания) за две предыдущие итерации менее заданного значения, т. е.
![]() . ( 4.1)
. ( 4.1)
В противном случае расчет повторяется заново (блок 10) с учетом изменения свойств материала под действием температуры (блок 9).
Результаты расчета представляют собой распределения напряжений и температур в зоне резания и отображаются на в виде диаграмм линий одинаковых напряжений и изотерм.
Существенно упростить предложенный алгоритм и уйти от итерационного процесса позволяет применение полуэкспериментального метода моделирования, заключающегося в том, что такие параметры процесса как например, силы резания и усадка стружки определяются экспериментально и являются входными данными для расчета НДС и температурных полей в зоне резания.
|
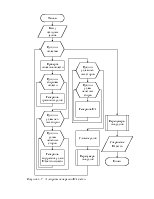
Рисунок 4.2 – Блок схема полуэкспериментального моделирования НДС и температурных полей в зоне резания нестационарных видов обработки |
Поскольку экспериментально определенные параметры уже учитывают влияние деформаций и температур на свойства материалов в зоне резания может быть принят линейный алгоритм (рисунок 4.2) последовательного расчета НДС и температурных полей. Однако указанный алгоритм требует проведения эксперимента и не является рациональным с экономической точки зрения. Более того, такой подход не позволяет прогнозировать характеристики процесса резания в области, где проведение экспериментов невозможно по тем или иным причинам.
В основу приведенных алгоритмов положены известные законы теорий пластичности, теплофизики и др. требующие для решения значительного объема вычислений. Однако современное развитие ЭВМ позволяют реализовать эти вычисления в короткие сроки.
Таким образом, представленный алгоритм моделирования процесса стружкообразования при нестационарных видах обработки и, в частности, при ТТ позволяет выполнить анализ деформационных и тепловых процессов в зоне стружкообразования и рассчитать упругопластические свойства обработанной поверхности не только в экспериментально исследованной области варьирования режимов обработки, но и в областях не допустимых для экспериментального исследования из-за различных факторов: недопустимого уровня вибраций, низкой стойкости инструмента из-за случайного (усталостно-адгезионного) разрушения и т.п. Кроме того, по полученным данным возможно выполнить анализ процессов, обуславливающих стойкость и надежность инструмента, динамическое состояние технологической системы и качества обработанной поверхности, что в свою очередь позволит определить оптимальные условия и параметры режима обработки.
1.2 Методика моделирования процесса образования стружки с применением метода КЭ
В современных условиях развития машиностроения специалисты в области механики сплошных сред и теории механической обработки все больше уделяют внимание построению математической модели процесса резания. В данном разделе рассмотрена возможность и особенности построения полуэкспериментальной математической модели для анализа деформационных процессов и процессов теплопередачи в зоне стружкообразования при свободном тангенциальном точении.
1.2.1 Выбор вида КЭ и генерация КЭ сетки расчетной модели
Решение поставленной задачи является частью предложенного в предыдущем пункте алгоритма (см. рисунок 4.2). Для ее реализации целесообразно применить метод конечных элементов (МКЭ), основные принципы которого описаны в разделе 3. В соответствии с этими принципами исследуемая область делится на конечное число дискретных элементов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.