Разрабатываемая методика предназначена для моделирования
прямоугольного резания. Поэтому решается плоская задача теории упругости, позволяющая
получать поля напряжений в исследуемом объекте в зависимости от условий
деформирования. Такой подход дает возможность выделить зону упругопластических
деформаций, и вполне приемлем для отработки методики. В рассматриваемой
методике рассматривается сечение системы резания главной секущей плоскостью.
Начало координат выбрано в точке пересечения следов передней и задней
поверхностей режущего клина. Координатные оси ориентированы в направлении
вектора главного движения (![]() ) и в радиальном
направлении (
) и в радиальном
направлении (![]() ), образуя прямоугольную декартову
систему координат. Кривизной поверхности резания, наблюдаемой при обработке
цилиндрических заготовок пренебрегаем (
), образуя прямоугольную декартову
систему координат. Кривизной поверхности резания, наблюдаемой при обработке
цилиндрических заготовок пренебрегаем (![]() ).
).
|
Рисунок 4.3 – Изопараметрические четырехугольные элементы: а) линейные, б) квадратичные |
Выбор типов применяемых КЭ является важным шагом , сильно влияющим на эффективность расчета. Простейшая форма идеализации двумерной задачи состоит в использовании треугольников с узлами, расположенными в вершинах. Эти элементы использовались в числе первых [69]. Впоследствии было замечено, что при увеличении числа степеней свободы, связанных с элементом, снижается общее число степеней свободы системы, необходимое для достижения заданной точности. Однако при использовании более сложных элементов возрастает время вычисления матриц жесткости элементов и увеличивается ширина ленты матрицы системы уравнений равновесия,. что также ведет к росту времени счета. В результате сравнения точного и приближенного решения тестовых задач было найдено, что наиболее эффективными с точки зрения точности и времени вычислений в условиях моделирования процесса резания являются изопараметрические четырехугольные КЭ (рисунок 4.3) [69, 77 и др.]. В данной работе в качестве базового используются изопараметрические четырехугольные линейные элементы (рис. 4.3,а). Эти элементы представляют собой четырехугольник общего вида. Пусть координаты узлов, перемещения и температура в узлах КЭ задаются векторами вида:
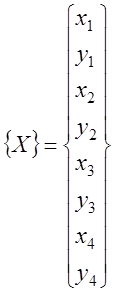 ;
; 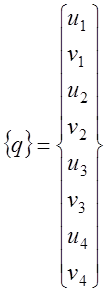 ;
; 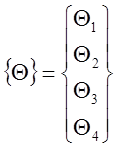 ,
( 4.2)
,
( 4.2)
Тогда в любой внутренней точке КЭ величина перемещения, температуры или ее координаты могут быть выражены через узловые значения:
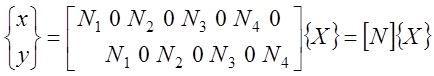 , (
4.3)
, (
4.3)
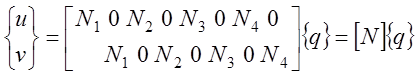 (
4.4)
(
4.4)
![]() ( 4.5)
( 4.5)
где 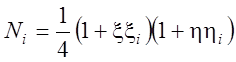 -
функции формы;
-
функции формы; ![]() ,
, ![]() -
локальные координаты (
-
локальные координаты (![]() ;
; ![]() );
);
![]() ,
, ![]() -
локальные координаты в узле i .
-
локальные координаты в узле i .
При построении полей заданной функции иногда бывает необходимо определить локальные координаты точки внутри элемента по известным глобальным координатам. Из выражения (4.3) получаем:
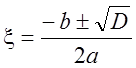 ;
; 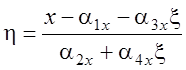 , (
4.6)
, (
4.6)
где
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
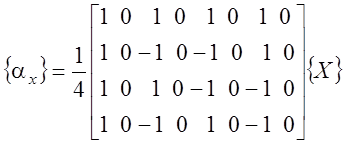 ;
; 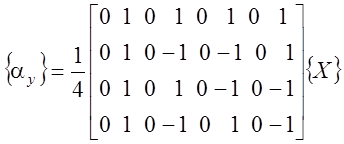 .
.
Таким образом, формирование КЭ сетки заключается в делении заданной геометрической модели системы резания на конечные элементы, т.е. определение координат узлов КЭ и описания сторон КЭ. При этом к КЭ предъявляются следующие требования:
1. Отношение длины к ширине КЭ должно стремиться к 1;
2. Углы КЭ должны по величине стремиться к 90°;
3. Должно быть минимальное число КЭ, описывающих заданную геометрическую модель;
4. КЭ сетка должна быть сгущена в местах наибольших градиентов деформаций или температуры;
5. КЭ сетка должна обеспечивать получение устойчивого решения, учитывая ожидаемые искажения КЭ при больших пластических деформациях.
Необходимо отметить, что при реализации решения пластической задачи возникает нестабильность вычислительного процесса. Одним из методов решения этой проблемы является применение треугольных КЭ.
Для обеспечения реальных условий деформирования и теплопередачи геометрическая модель описывает достаточно большую область заготовки, стружки и инструмента. Однако градиенты изменения исследуемых функций в большей части этой области незначительны и могут быть описаны меньшим числом элементов. В тоже время КЭ сетка, в соответствии с принципами Дж. Стренковского [62] формирования КЭ сетки в условиях больших пластических деформаций, должна иметь регулярную структуру. Поэтому из всех известных методов формирования КЭ сетки был выбран метод прямого построения в четырехугольной области с в возможностью искажения и сгущения сетки у одной из сторон.
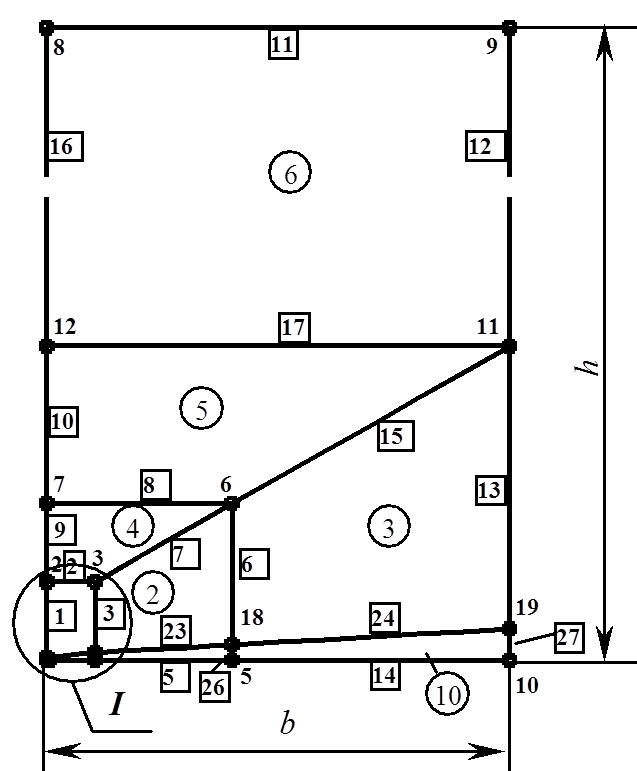
Для уменьшения времени счета и экономии машинной памяти в вычислительной процедуре участвует только ограниченная область около текущего положения режущей кромки (РК) [62]. В данной работе формирование КЭ сетки осуществляется по заранее сформированной геометрической модели, состоящей из укрупненных четырехугольных областей (см. рисунки 4.4 и 4.5). Координаты узловых точек определялись по соотношениям, приведенным в таблице 4.1
|
|
|
|
Здесь текущая и максимальная толщина среза определялись
по формуле (2.1), кинематические передний и задние
углы по формуле (2.8), длина контакта в первом приближении по формуле (3.16). В процессе решения задачи длина контакта по передней поверхности уточняется.
Коэффициент укорочения стружки ![]() определялся экспериментально
по методике, представленной в разделе 5.
определялся экспериментально
по методике, представленной в разделе 5.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.