Методики моделирования нестационарного процесса тангенциального точения, страница 3

В литературе отмечается, что при малых толщинах среза значительно влияние радиуса округления режущей кромки на НДС в зоне стружкообразования. Поэтому в рассматриваемой модели предусмотрен учет радиуса округления РК, который представлен периметром трапеции с вершинами принадлежащими дуге округления. Координаты вершин рассчитывались по формулам (рисунок 4.6):

, ;        ( 4.7)

, .        ( 4.8)

Необходимо отметить,. что требование обеспечения устойчивости получаемых решений при расчете НДС и температурного поля различны. Поэтому для решения указанных задач требуется различная КЭ сетка.

В данной работе предложен алгоритм формирования КЭ сетки с возможностью трехкратного сгущения узлов у одной из сторон разбиваемой области и непрерывным изменением размеров сторон КЭ вдоль любой из сторон разбиваемой области (рисунок 4.7). Исходными данными являются координаты узловых точек геометрической модели определенные по формулам таблицы 4.1, описание сторон областей с указанием параметра сгущения  и количества элементов  на этой стороне и описание самих областей в виде списка принадлежащих им сторон. Возможны два варианта КЭ сетки:

Таблица 4.1– Формулы для определения координат характерных точек геометрических моделей  и величин проекций скоростей материала в этих точках № точки X Y VX VY Инструмент (рисунок 4.4) 1 0 0 0 0 2 0 Cmax 0 0 3 ha Cmax 0 0 4 ha 0 0 0 8 0 h 0 0 9 b h 0 0 10 b 0 0 0 13 r 0 0 0 14 0 r 0 0 15 0 0 16 0 0 Заготовка (рисунок 4.5) 1 0 0 VC×sin(g) || V×cos(a)   VC×cos(g) || V×sin(a) 2 ht×cos (Yt -a ) ht×sin (Yt -a ) V×cos(a)  ||  V V×sin(a)  ||  0 4 10× amax 0 V 0 6 10× amax -5×amax V 0 12 -5× amax -5× amax V 0 22 -5× amax at(nt + Dnt) V 0 17 - at / tg(F) at V   ||  VC×sin(g) 0   ||  VC×cos(g) 18 X21 - at×cos (g) /KL Y21 + at×sin (g) / KL VC×sin(g) || VC×sin(g1) VC×cos(g) || VC×cos(g1) 19 X20 - at×cos (g) /KL Y20 + at×sin (g) / KL VC×sin(g1) VC×cos(g1) 20 X21 + 2×amax ×sin (g1) Y21+2×amax ×cos (g1) VC×sin(g1) VC×cos(g1) 21 Ct×sin(g) Ct×cos(g) VC×sin(g) || VC×sin(g1) VC×cos(g) || VC×cos(g1) где     g1 = g + 10°; ;   - максимальная ширина фаски износа.

равномерная КЭ сетка формируется, когда на противоположных сторонах указанно одинаковое число узлов (рисунок 4.8,а) и; 2) сгущенная КЭ сетка формируется, когда указанное количество узлов на одной из сторон в три раза больше, чем у противоположной (рисунок 4.8,б). Другие варианты считаются недопустимыми.

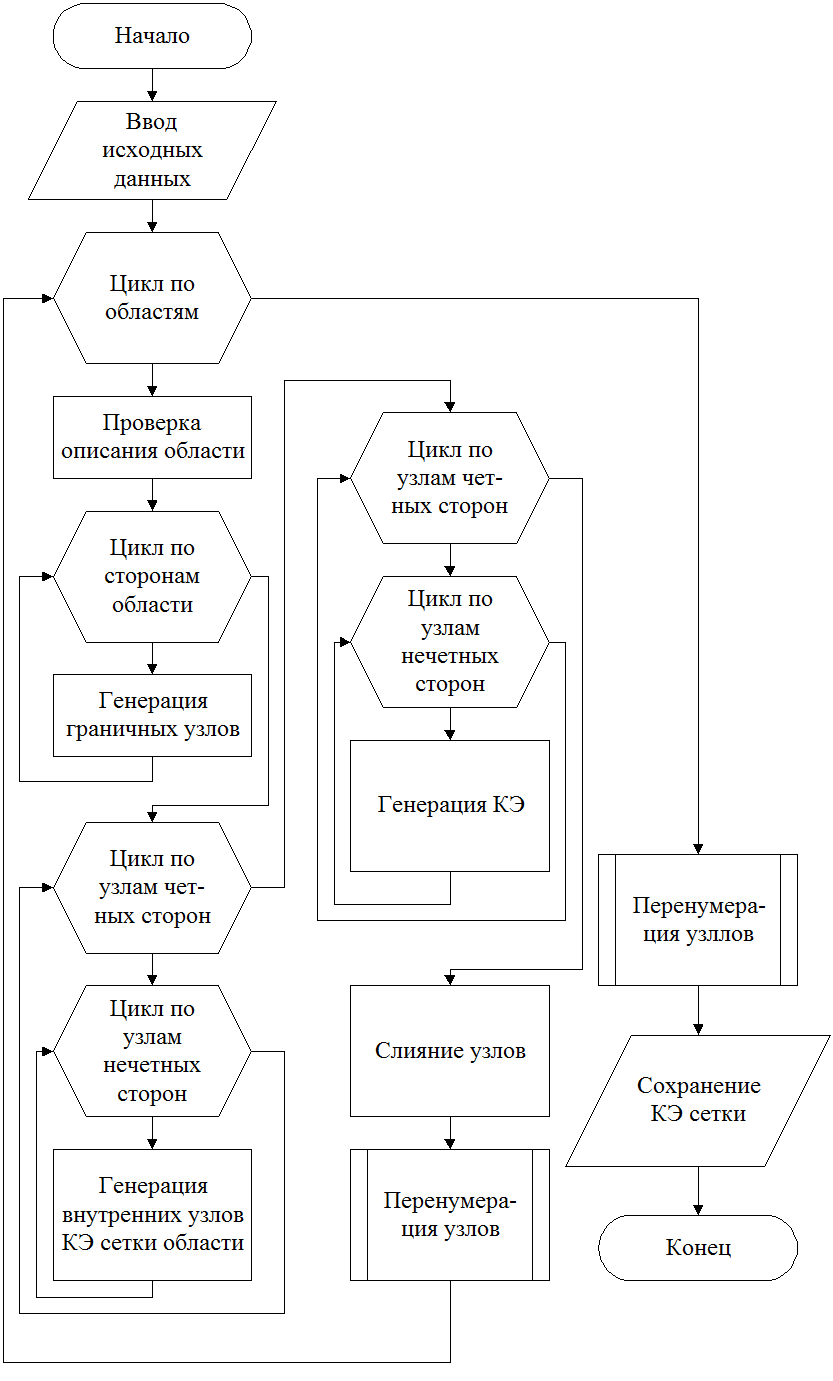
Рисунок 4.7 – Алгоритм генерации КЭ сетки

Рассмотрим алгоритм по блокам:

блок 1 – начало алгоритма;

блок 2 – ввод исходных данных;

блок 3 – цикл по областям. Просматриваются все области заданной геометрической модели с целью формирования КЭ сетки;

блок 4 – проверка корректности введенных данных и приведение описания области к нормальному виду. Нумерация сторон начинается со стороны с максимальным числом узлов;

блок 5 – цикл по сторонам разбиваемой области;

блок 6 – на стороне, как на отрезке с заданными координатами концов (; ) генерируется  узлов в соответствии с заданным параметром сгущения , представляющем собой основание геометрической прогрессии, т.е.