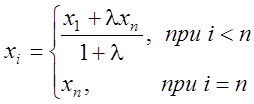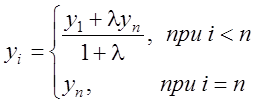Машиностроение \ Режущий инструмент

Методики моделирования нестационарного процесса тангенциального точения, страница 4

;                                       ,( 4.9)

где ; ; ; ;

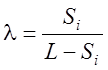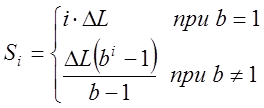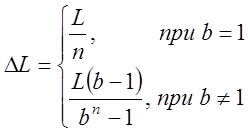         - длина стороны.

Необходимо заметить, что при формировании сгущенной КЭ сетки формируются дополнительные узлы.

блок 7 и 8 – цикл по узлам соответственно четных и нечетных сторон области

блок 9 – генерация внутренних узлов КЭ сетки области, как точек пересечения отрезков соединяющих соответствующие узлы на сторонах КЭ:

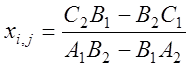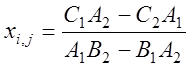; ;                                ,( 4.10)

где     ; ; ;

          ; ; .

блок 10 и 11 – цикл по узлам соответственно четных и нечетных сторон

блок 12 – генерация конечных элементов. Элемент составляется из узлов с номерами , , ,  в следующем порядке:

; ; ; .          ( 4.11)

Необходимо отметить, что при наличии сгущения в алгоритм описания элементов вводится поправка;

блок 13 – слияние узлов с координатами, удовлетворяющими условию:

,                                                ( 4.12)

где e = 0,0001 – допустимая погрешность слияния;

блок 14 – перенумерация узлов. Узлы не принадлежащие ни одному элементу исключаются из списка;

блок 15 – перенумерация узлов. На этом этапе исключаются из списка узлы высвобожденные в результате слияния;

блок 16 – сохранение сформированной КЭ сетки;

блок 17 – конец.

Получаемая КЭ сетка представлена на рисунке 4.8. Как видно предлагаемы алгоритм позволяет почти в три раза уменьшить количество КЭ в зоне далекой от РК, не нарушая при этом упорядоченность и целостность КЭ сетки.

Известно, что при решении нестационарного уравнения теплопроводности в случае наличия значительных градиентов температур возникают т. н. колебания числовых значений температурного поля, часто приводящие к получению физически некорректных результатов даже тогда, когда метод счета сам по себе устойчив [[ii]]. Эти искажения можно свести к минимуму, сформировав КЭ сетку, сгущенную в местах ожидаемых больших градиентов температуры – у границ контактов на передней и задней поверхностях, - подобрав при этом оптимальное сочетание шага интегрирования и размеров КЭ в направлении этого градиента (рисунке 4.9).

Рисунок 4.9 - Сгущение КЭ сетки у режущей контактных поверхностей для случая решения задачи о теплопередаче

При анализе нестационарных процессов часто прибегают к замене непрерывно изменяющегося параметра его средними значениями в отдельные интервалы времени продолжительностью Dti, на каждом из которых считается, что происходит установившийся процесс резания с постоянным значением параметра, величина которого равна среднему его значению на данном интервале. Это дает возможность выполнять расчет только в конечном числе точек цикла обработки.

Длительность каждого участка в общем случае может быть произвольной и определяется необходимой точностью, градиентом изменения величины на этом участке и методом расчета.

Так для расчета НДС целесообразно вычислять длительность интервала из условия равного приращения толщины среза по формуле:

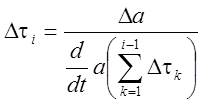,                                                    (4.13)

где - заданное приращение толщины среза, причем  ; .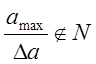

Рисунок 4.10 – Схема определения расчетных точек  цикле обработки

На рисунке 4.10 представлены результаты такого преобразования по формуле (4.13). При этом за расчетные точки принимаем точки, соответствующие середине полученных интервалов. Величины сил и усадки стружки в этих точках принимаем равными их средним значениям на интервалах, определенных из осциллограмм; значение толщины среза и кинематических углов рассчитываем по формулам (2.1) и (2.8) в расчетных точках.

Однако при анализе тепловых процессов более удобно разделить цикл обработки на равные интервалы Dti , что существенно упрощает расчетные формулы, хотя и дает некоторую погрешность в связи с различным градиентом изменения параметров резания в течение цикла обработки.


1.2.2  Реализация на ЭВМ

Для выполнения расчетов по описанным математическим моделям в работе за основу взято универсальное программное обеспечение. Среди множества существующих пакетов (см. раздел 3.3.3) был выбран пакет NISA II/DISPLAY III, поскольку является наименее требовательным к аппаратному обеспечению ЭВМ и обладает достаточным набором инструментов.

В тоже время прямое применение этого макета для моделирования процесса ТТ невозможно по описанным ранее в разделах 2 и 3 причинам. Поэтому было разработано специальное программное обеспечение позволяющее приспособить пакет NISA II/DISPLAY III к решению поставленной задачи.

Разработанное программное обеспечение включает в себя формирование геометрической модели и КЭ сетки по описанным в разделе 4.2.1 правилам и алгоритмам, подготовку расчетной схемы и обработку результатов, а также реализован алгоритм расчета температурного поля, представленный на рисунке 4.11.

Описанное программное обеспечение было разработано на языке Watcom C++ для Windows 95, что позволило существенно повысить скорость вычислений. Программный пакет состоит из модулей формирования КЭ сетки инструмента (toolmesh.exe), формирования КЭ сетки заготовки и стружки (workmesh.exe), сборки КЭ модели (join.exe), модуля обновления начального поля температуры (shift.exe), модуля формирования файла данных для модулей “nisa2.exe” и “heat.exe” пакет NISA II/DISPLAY III, а также модуля просмотра результатов расчета (meshview.exe). Исходные данные задаются в текстовом файле данных (test.ini). Листинг основных модулей приведен в приложении Б.

Скачать файл