Математическая модель обрабатываемого и инструментального материала при разработке модели процесса резания

Вопрос о математической модели как обрабатываемого так и инструментального материала очень важен при разработке модели процесса резания. В результате проведенных исследований разработано огромное число моделей материалов, однако только некоторые из них более или менее точно описывают весь спектр свойств присущих реальному материалу. Среди них наиболее часто при исследовании процессов резания пластичных материалов применяют упруго-пластическая среда с линейным упрочнением (рис. 3.10, а). Для этой реологической модели уравнение состояния принимает вид [[i]]:

,

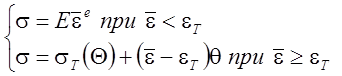где  - модуль упрочнения.

Однако в ряде случаем удобно применять жестко-пластическую среду Мизеса, изображающую свойство абсолютной пластичности. Механическая модель –  элемент трения (рис. 3.10, б); а уравнение состояния имеет вид:

;

Известно два условия наступления пластического состояния при объемном напряженном состоянии. Это условие пластичности Треска Сен-Венана и энергетическое условие пластичности Губера-Мизеса. Последнее довольно хорошо подтверждается экспериментом и может быть представлено в виде:

.                      ( 3.25)

Особое значение приобретает вопрос о выборе критерия разрушения. В настоящее время известно два вида разрушения. Оба вида разрушения включают в себя образование малых по величине трещин внутри напряженного твердого тела с последующим распространением одной или нескольких трещин через все тело. Главное различие механизмов разрушения заключается в природе распространения трещин. В случае вязкого разрушения развитие трещины связано с явлением пластического течения, а хрупкое разрушение является процессом скалывания с очень незначительным объемом пластических деформаций. Вероятность хрупкого разрушения увеличивается с уменьшением температуры и увеличением скорости деформаций [[ii]]. Критерии разрушения носят частный характер для данной группы материалов.

Интересно заметить, что как механические так и теплофизические характеристики материалов зависят от температуры. Известно, что с увеличением температуры модуль Юнга, предел текучести и другие механические характеристики, как правило, уменьшаются, но эта зависимость может иметь и экстремальный В тоже время коэффициент теплопроводности и теплоемкость для разных сталей и сплавов могут как увеличиваться, так и уменьшаться в зависимости от состава [33]. Хорошо известно, что для сталей с повешением температуры свойственны фазовые превращения. Несмотря на то, что они протекают с относительно малой скоростью, они могут оказать свое влияние при достаточно высоких степенях перегрева, наблюдаемых при обработке твердыми сплавами. При этом в критических точках свойства материала изменяются скачкообразно (рисунок 3.11) [[iii]].

Таким образом, обрабатываемый материал может характеризоваться следующими свойствами и их зависимостью от температуры:

- механическими:  - модуль Юнга;  - коэффициент Пуассона;                - предел текучести примерно равный условному пределу текучести при 0.01% пластической деформации;  - временное сопротивление;  - истинное напряжение при разрыве;  - модуль упрочнения;  - коэффициент линейного расширения;  - плотность;

- теплофизическими:  - коэффициент теплопроводности; - теплоемкость.

При высокопроизводительной обработке металлов резанием в промышленности широко применяется твердосплавный инструмент групп ВК, ТК, ТТК. Разрушение режущей части инструмента под действием нагрузок, определяемых как силами резания так и тепловым состоянием системы, исходя из возникающего в ней напряженного состояния, характеризуется следующими показателями прочности: s_в, s_-в, s_0.01 и др. В настоящее время хорошо известно, что все эти характеристики материала сильно зависят от температуры, что несомненно должно учитываться при анализе прочности режущей части инструмента.