Методика расчета температуры резания при ТТ методом источников
В данном разделе рассмотрено применение метода источников к теплофизическому анализу нестационарных процессов резания на примере процесса ТТ. Приводятся алгоритм и программа расчета средней температуры резания за цикл обработки при ПТТ.
Описание и теоретическое обоснование методики
При резании металлов температура на передней и задней поверхностях инструмента с использованием метода источников рассчитывают в 2 этапа [48]:
– определение температур на поверхностях стружки и заготовки в предположении, что резец нетеплопроводен;
– определение интенсивности тепловых потоков, переходящих в резец, и температуры на поверхностях инструмента с учетом теплопроводности резца.
Считая все параметры зависимыми от времени, рассмотрим расчет температуры резания при ТТ.
Введем следующие допущения: 1) цикл обработки и характер изменения толщины среза соответствуют теоретическому; 2) свойства материалов не зависят от температуры; 3) вследствие кратковременности контакта инструмента с заготовкой и отсутствия СОЖ, пренебрегаем теплообменом системы с окружающей средой; 4) резание происходит с высокими скоростями при отсутствии наростообразования; 5) не учитываем теплоту трения на задней поверхности.
Температура в любой точке зоны резания есть результат воздействия трех источников тепла: теплоты трения на участке контакта «резец-стружка», теплоты деформации и теплоты трения на участке контакта «резец-заготовка».
|
Рисунок 4.16– Структурная схема теплообмена |
В соответствии со структурной схемой теплообмена (рисунок
4.16) выполним схематизацию системы резания. Инструмент представлен в виде
неограниченного клина с углом заострения b
и углом при вершине e = 90° (![]() ). Заготовка, представлена
полупространством, движущимся относительно инструмента со скоростью резания V.
Сливная стружка представлена в виде бесконечного стержня, движущегося
относительно инструмента со скоростью резания
). Заготовка, представлена
полупространством, движущимся относительно инструмента со скоростью резания V.
Сливная стружка представлена в виде бесконечного стержня, движущегося
относительно инструмента со скоростью резания 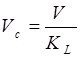 с учетом принятых допущений [48].
с учетом принятых допущений [48].
По поверхности контакта «резец-стружка» относительно стружки действуют следующие источники теплоты, описанные в разделе . Плотность распределения этих источников рассчитываем по формулам (3.21), (4.58), (4.69) и (4.67) в виде:
![]() ;
; ![]() ;
;
![]() , ( 4.71)
, ( 4.71)
Принимаем для условий
обработки конструкционной углеродистой стали при скоростях ![]() м/с
м/с ![]() и
и
![]() , что хорошо согласуется с
проведенными автором экспериментами.
, что хорошо согласуется с
проведенными автором экспериментами.
Кроме того на поверхностях контакта действуют стоки теплоты:
–
сток теплоты в инструмент интенсивностью ![]() с равномерным законом распределения.
Его мощность вычисляется по формуле:
с равномерным законом распределения.
Его мощность вычисляется по формуле:
![]() . (
4.72)
. (
4.72)
–
сток теплоты в инструмент интенсивностью ![]() с равномерным законом распределения.
Его мощность вычисляется по формуле:
с равномерным законом распределения.
Его мощность вычисляется по формуле:
![]() . (
4.73)
. (
4.73)
Пусть в стружку переходит часть теплоты, в виде потока ![]() , равная [48]
, равная [48]
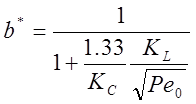 , (
4.74)
, (
4.74)
где ![]() - коэффициент формы;
- коэффициент формы; 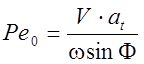 - безразмерный
критерий Пекле. Остальная часть теплоты деформации переходит в заготовку в виде
потока
- безразмерный
критерий Пекле. Остальная часть теплоты деформации переходит в заготовку в виде
потока ![]() .
.
Тогда, интенсивность источника деформирования относительно стружки рассчитывается по формуле:
![]() , (
4.75)
, (
4.75)
Рассмотрим теплообмен по передней поверхности резца,
полагая ![]() .
При этом средняя температура резания будет равна средней температуре на
площадке контакта стружки с резцом.
.
При этом средняя температура резания будет равна средней температуре на
площадке контакта стружки с резцом.
Представляем непрерывную функцию изменения толщины среза
в виде массива ее значений через равные интервалы времени ![]() . В эти же моменты времени цикла
обработки из эксперимента определяем силы резания и коэффициент укорочения
стружки по методике, описанной в разделе 5 и составляем уравнения для расчета интенсивности
источников теплоты (
. В эти же моменты времени цикла
обработки из эксперимента определяем силы резания и коэффициент укорочения
стружки по методике, описанной в разделе 5 и составляем уравнения для расчета интенсивности
источников теплоты (![]() и
и ![]() )
по формулам (4.71). Тогда из условия равенства средних температур в данный
момент времени на прирезцовой стороне стружки
)
по формулам (4.71). Тогда из условия равенства средних температур в данный
момент времени на прирезцовой стороне стружки ![]() и передней поверхности
и передней поверхности ![]() составляем
уравнение:
составляем
уравнение:
![]() , (4.76)
, (4.76)
где ![]() ,
, ![]() - итоговые тепловые потоки на
площадках контакта соответственно стружки с инструментом и заготовки с
инструментом в момент времени
- итоговые тепловые потоки на
площадках контакта соответственно стружки с инструментом и заготовки с
инструментом в момент времени ![]() (
(![]() ,
, ![]() -
количество интервалов).
-
количество интервалов).
Аналогичное уравнение составляем из условия равенства
средних температур на обработанной поверхности заготовки ![]() и задней поверхности
и задней поверхности ![]() :
:
![]() , (4.77)
, (4.77)
Согласно принятых допущений ![]() и
и ![]() рассчитываем по формулам [48]:
рассчитываем по формулам [48]:
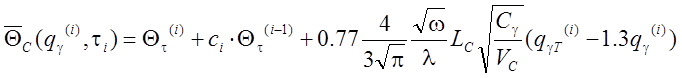 (4.78)
(4.78)
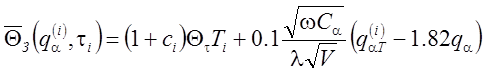 (
4.79)
(
4.79)
где 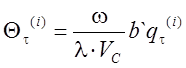 - температура деформации в момент
времени
- температура деформации в момент
времени ![]() ; с – коэффициент, учитывающий
подогрев поверхностных слоев материала, из которого образуется стружка;
; с – коэффициент, учитывающий
подогрев поверхностных слоев материала, из которого образуется стружка;![]() , LM
- коэффициенты формы;
, LM
- коэффициенты формы; ![]() - функция, отображающая
температур, вызванных теплотой деформации, на площадке контакта заготовки с инструментом;
- функция, отображающая
температур, вызванных теплотой деформации, на площадке контакта заготовки с инструментом;
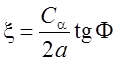 .
.
Коэффициенты формы определяются по формулам [48]:
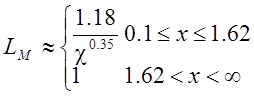 (
4.80)
(
4.80)
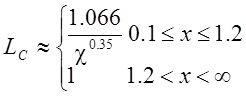 (
4.81)
(
4.81)
В виду наличия особенностей, отличающих процесс ТТ от
традиционных методов обработки коэффициент подогрева ![]() определяем
из следующих соображений. В любой момент времени
определяем
из следующих соображений. В любой момент времени ![]() в
стружку направлена
в
стружку направлена ![]() часть теплоты
деформирования
часть теплоты
деформирования ![]() , а в заготовку -
, а в заготовку - ![]() часть теплоты деформирования
часть теплоты деформирования ![]() . Учитывая высокую скорость резания
(80–400 м/мин) при ТТ рассматриваемую систему (источник теплоты, вызванный
деформациями в зоне резания, на заготовке) можно упрощенно представить в виде
плоского мгновенного источника теплоты на торце неограниченного стержня с
адиабатической боковой поверхностью, вносящего в момент времени
. Учитывая высокую скорость резания
(80–400 м/мин) при ТТ рассматриваемую систему (источник теплоты, вызванный
деформациями в зоне резания, на заготовке) можно упрощенно представить в виде
плоского мгновенного источника теплоты на торце неограниченного стержня с
адиабатической боковой поверхностью, вносящего в момент времени ![]()
![]() теплоты.
Тогда температура на расстоянии
теплоты.
Тогда температура на расстоянии ![]() от торца стержня в
момент времени
от торца стержня в
момент времени ![]() равна [48]:
равна [48]:
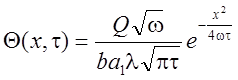 , (4.82)
, (4.82)
где ![]() -
ширина срезаемого слоя;
-
ширина срезаемого слоя; ![]() - толщина
стружки.
- толщина
стружки.
За время одного оборота ![]() (
(![]() - частота вращения заготовки), на
подогрев слоя материала заготовки толщиной
- частота вращения заготовки), на
подогрев слоя материала заготовки толщиной ![]() пойдет
часть теплоты равная:
пойдет
часть теплоты равная:
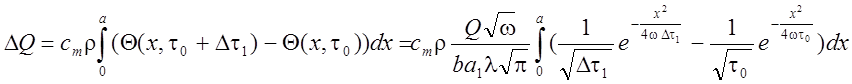 . (4.83)
. (4.83)
Обозначив 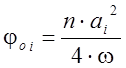 , после
преобразований получаем:
, после
преобразований получаем:
![]() , (4.84)
, (4.84)
где 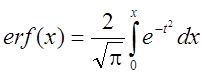 .
.
Тогда коэффициент ![]() определяется
формулой:
определяется
формулой:
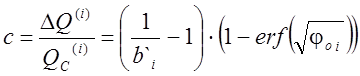 . (4.85)
. (4.85)
Расчеты показывают, что коэффициент ![]() , являясь переменным в течение цикла
обработки, может изменяться от 0.1 до 0.85, что значительно превышает его
значения для традиционных методов обработки [32].
, являясь переменным в течение цикла
обработки, может изменяться от 0.1 до 0.85, что значительно превышает его
значения для традиционных методов обработки [32].
|
|
|
Рисунок 4.17– Изменение коэффициента подогрева в течение цикла обработки |
Среднюю температуру на передней поверхности определяем из выражения [48]:
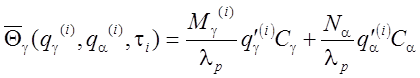 , (4.86)
, (4.86)
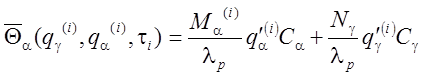 ( 4.87)
( 4.87)
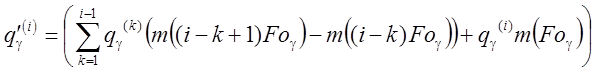 , (4.88)
, (4.88)
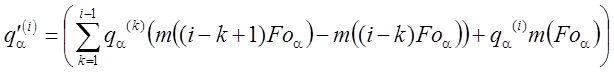 , ( 4.89)
, ( 4.89)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.