Байесовские сети как инструмент поддержки принятия решений в условиях неопределённости, страница 9

На основе экспертной оценки начальное состояние оборудования (перед 1-м месяцем) может быть хорошим с вероятностью 0.4, удовлетворительным с вероятностью 0.5 и плохим с вероятностью 0.1.

При построении диаграммы влияния рекомендуется применять объектно-ориентированный подход (см. работу № 1).

По полученной диаграмме влияния найдите оптимальную ситуационную политику проведения профилактических мер.

Допустим теперь, что предприятие до начала четырёхмесячного цикла рассматривает вопрос о целесообразности обновления оборудования. Тогда, если приобрести новое, то в случае хорошего состояния старого оборудования придётся доплатить разницу в 1000 у. е., в случае удовлетворительного ― 1500 у. е., а в случае плохого ― 5000 у. е.

Если оставить старое, по истечении четырёх месяцев нужно провести его капитальный ремонт. В случае хорошего состояния оборудования этот ремонт может обойтись в 1000 у. е., в случае удовлетворительного ― в 1250 у. е., а в случае плохого ― в 2000 у. е. Состояние нового оборудования на 95 % может быть хорошим, а при наличии каких-то скрытых дефектов: на 4.9 % ― удовлетворительным и на 0.1 % ― плохим.

Дополните построенную ранее диаграмму влияния новыми переменными и определите, целесообразно ли проводить замену оборудования и какова будет в данном случае оптимальная политика профилактической деятельности.

Отчёт должен содержать: цель работы; постановку задачи; распечатку структуры диаграммы влияния c семантической интерпретацией вершин; словесную формулировку оптимальной политики (см. пример 2) профилактической деятельности в исходном случае и в случае с заменой оборудования (привести также оценки полезности выбора альтернатив при вершинах решений); краткий вывод по проделанной работе.

Лабораторная работа № 3

СМЕШАННЫЕ БАЙЕСОВСКИЕ СЕТИ В РЕШЕНИИ УПРАВЛЕНЧЕСКИХ ЗАДАЧ С НАЛИЧИЕМ НЕОПРЕДЕЛЁННОСТИ

Цель работы: изучение теоретических основ смешанных байесовских сетей (сетей с непрерывными случайными переменными) в среде ИЭС Hugin Lite; приобретение практических навыков представления знаний и данных в условиях неопределённости на основе смешанных байесовских сетей.

Общие сведения

В байесовских сетях наряду с дискретными можно задавать также и непрерывные случайные переменные. Сети, содержащие оба типа вершин, называют смешанными или гибридными (mixed (hybrid) bayesian networks). При этом для точного расчёта необходимы следующие ограничения: непрерывные переменные должны иметь нормальный закон распределения , а дискретные переменные не должны иметь непрерывных родителей, дисперсия условного распределения непрерывных переменных не зависит от дисперсии непрерывных родителей.

Функцию плотности случайной величины с нормальным законом распределения в литературе также называют гауссианой:

.

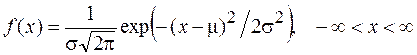Методы приближённого расчёта, непосредственно способные работать и с другими известными распределениями, в Hugin Lite 6.1 не поддерживаются, однако теоретически с заданной погрешностью широкий спектр непрерывных распределений можно представить в виде смеси гауссиан.

Итак, общее множество вершин сети , где  ― подмножество вершин дискретных и  ― непрерывных переменных. Дискретные вершины специфицируются так же, как в БСД. Для непрерывных задаётся семейство условных плотностей распределения от непрерывных родителей при каждом сочетании состояний дискретных:

, где  ― вектор с размерностью равной числу непрерывных родителей; число  и вектор весовых коэффициентов  ― параметры условного математического ожидания;  ― условная дисперсия.

Это выражение можно интерпретировать как линейное уравнение множественной регрессии со стохастическими регрессорами:

, где , .