Байесовские сети как инструмент поддержки принятия решений в условиях неопределённости, страница 10

Заметим, что механизм расчёта, заложенный в Hugin, позволяет вводить и вершины, задающие неискажённую линейную функцию от родителей, т. е. , если задать . Так можно ввести вершину, задающую неискажённую сумму нескольких случайных величин.

Параметры  и  априорного распределения  непрерывных вершин без родителей задаются явно, для остальных они должны быть найдены в процессе расчёта. При этом маргинальная плотность есть . Она представляет собой смесь гауссиан, что позволяет получать точные значения её первых двух моментов. Таким образом, для непрерывной вершины целевыми расчётными характеристиками являются математическое ожидание и дисперсия. Эти характеристики позволяют оценить возможный интервал вариации значений случайной величины на основе теоремы Чебышева, которая гласит: вероятность того, что отклонение случайной величины по модулю от своей средней больше заданного числа , не превышает её дисперсии, делённой на квадрат этого числа, т. е. . Задавая определённую граничную вероятность, можно найти соответствующее ей отклонение: .

В качестве свидетельств в смешанных сетях выступает информация о том, что случайные переменные, соответствующие вершинам сети, принимают конкретные значения: для дискретной это один из её исходов (состояний вершины) , для непрерывной ― её численное значение . Тогда апостериорная смешанная плотность вычисляется как

, где  ;  .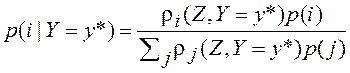

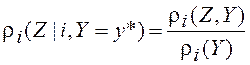Непрерывные переменные задают вариацию количественных параметров задачи и причинно-следственные зависимости в форме линейной регрессии. Дискретные же описывают качественные характеристики и неопределённость правил.

Содержание работы

1. Изучение БСД в среде ИЭС Hugin Lite на показательном примере.

Пример. Рассмотрим небольшую практическую задачу, которая решается с применением смешанных байесовских сетей.

Требуется отслеживать состояние очистительного фильтра на выходе печи для сжигания промышленных или бытовых отходов. На рис. 3.1 представлена структура сети. Вершины с двойной окружностью соответствуют непрерывным переменным, как принято в Hugin. Здесь переменная E ― эффективность фильтра, зависящая от типа сжигаемых отходов W = < industrial, household > (промышленный, бытовой) и состояния фильтра F = < intact, defect > (исправный, дефектный); M ― концентрация тяжёлых металлов в отходах; D ― концентрация дуста на выходе фильтра, зависящая от его пропускной способности (), от типа сжигаемых отходов и от режима сгорания B = < stable, unstable > (стабильный, нестабильный), определяемого по значению концентрации C углекислого газа в дыму на выходе трубы. Концентрация дуста измеряется по показаниям индикатора проницаемости L () и влияет на концентрацию тяжёлых металлов на выходе M_о, зависящей от их изначальной концентрации в отходах и концентрации дуста (m_о=m ). Требуется сделать заключение о состоянии фильтра F и величине эмиссии тяжёлых металлов M_o и дуста D на основе информации о W и измерений C и L. Непрерывные переменные имеют логарифмически нормальное распределение, аппроксимируемое нормальным распределением их логарифмов. Это позволяет перейти от мультипликативных зависимостей к аддитивным линейным и построить смешанную байесовскую сеть.

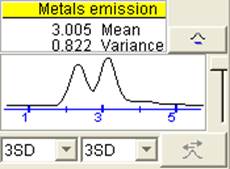
Рис. 3.1                                     Рис. 3.2

Откройте файл «wast.net» и ознакомьтесь с моделью. Обратите внимание на то, каким образом заданы условные распределения для непрерывных вершин.

В режиме исполнения проследим как работает данная модель. Слева в общем списке непрерывные вершины представлены математическим ожиданием и дисперсией. Однако, прежде всего в случае смешанного распределения, полную картину вариации зачастую даёт лишь график плотности вероятностей. Чтобы вывести график, надо использовать «Monitor Window» (рис. 3.2).