- «ЕСЛИ свечи зажигания в порядке ТО “В СЛУЧАЕ силы тока: а) расчётной: ″ЕСЛИ цепь исправна (нет утечки) ТО богатая искра с вероятностью 1 ИНАЧЕ слабая искра с вероятностью 0.25 или нет искры с вероятностью 0.75″; б) пониженной: ″ЕСЛИ цепь исправна (нет утечки) ТО богатая искра с вероятностью 0.1 или слабая искра с вероятностью 0.9 ИНАЧЕ слабая искра с вероятностью 0.1 или нет искры с вероятностью 0.9″; в) недопустимо малой: нет искры” ИНАЧЕ искра не вырабатывается»;
- «ЕСЛИ топливная система исправна И в бензобаке есть бензин ТО топливо подаётся с вероятностью 1 ИНАЧЕ топливо не подаётся»;
- «ЕСЛИ двигатель проворачивается И топливо подаётся ТО “В СЛУЧАЕ искры: а) богатой: ″ЕСЛИ распределитель зажигания отрегулирован ТО двигатель заводится с вероятностью 1 ИНАЧЕ двигатель заводится с вероятностью 0.6″; б) слабой: ″ЕСЛИ распределитель зажигания отрегулирован ТО двигатель заводится с вероятностью 0.5 ИНАЧЕ двигатель заводится с вероятностью 0.1″; в) при отсутствии искры: двигатель не заводится” ИНАЧЕ двигатель не заводится».
Априорные вероятности неисправностей: для распределителя зажигания ― 0.05, для свечей ― 0.1, для электропроводки ― 0.05 при нормальной температуре, 0.1 при высокой и 0.8 при очень высокой.
Формализуйте данную систему правил в виде БСД и построенную сеть интегрируйте в модель <cаr_start_2> в рамках объектно-ориентированного подхода. Проанализируете ситуации, когда двигатель не запускается: 1) в дороге, долго проработав; 2) в гараже. Каково в этих ситуациях будет доверие к исправному состоянию устройств, представленных в модели, если бензобак не пуст, фары горят, аккумулятору год и индикатор не зажигается в ситуациях, когда: а) двигатель прокручивается и б) не прокручивается, и есть основания полагать, что шансы хорошего состояния аккумулятора в отношении других составляют «2 к 1» (недавно была профилактическая подзарядка) ?
Отчёт должен содержать: цель работы, постановку задачи, распечатку структуры ООБС и отдельных БСД c семантической интерпретацией вершин и протокол работы сети (списки вероятностей состояний вершин) в заданных ситуациях, а также краткий вывод по проделанной работе.
Лабораторная работа № 2
ДИАГРАММЫ ВЛИЯНИЯ И ПОДДЕРЖКА ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЁННОСТИ
Цель работы: изучение теоретических основ диаграмм влияния и принципов работы с ними в среде ИЭС Hugin Lite; приобретение навыков в формализации процедур принятия решений в условиях неопределённости с помощью диаграмм влияния.
Общие сведения
Диаграммы влияния (a Influence Diagramms ) ― это формализм, расширяющий БСД понятиями полезности и решения (decisions).
Если БСД содержали только один тип вершин, которые называются «вершинами шансов» (a chance node) и соответствуют состояниям случайных переменных, то в диаграммах влияния (ДВ) используются ещё два типа вершин:
- «вершины решения» (a decisions node), обозначаемые в ДВ прямоугольником;
- «вершины полезности» (a utility node), обозначаемые в ДВ ромбом.
Непрерывные переменные в ДВ не поддерживаются.
Каждая вершина полезности имеет локальную функцию полезности, которая связывает каждую комбинацию состояний её родителей с ожидаемой полезностью, заданной дискретным распределением. Общая функция полезности сети определяется как сумма локальных функций.
Родителями вершин полезности могут быть как вершины решений, так и вершины шансов, но сами они не могут иметь дочерних вершин.
Значение средней ожидаемой полезности ![]() заданной вершины
полезности
заданной вершины
полезности ![]() при условии
при условии ![]() и предшествующих решениях
и предшествующих решениях
![]() вычисляется так:
вычисляется так:
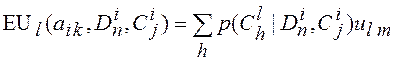 , где
, где ![]() ― вероятность
― вероятность ![]() -го сочетания состояний
вершин шансов
-го сочетания состояний
вершин шансов ![]() ― родителей
― родителей ![]() при
условии
при
условии ![]() и предшествующих решениях
и предшествующих решениях
![]() ;
; ![]() ― заданная заранее условная полезность вершины
― заданная заранее условная полезность вершины ![]() при
при ![]() -м сочетании состояний её
родителей
-м сочетании состояний её
родителей ![]() , соответствующем
, соответствующем ![]() и
и ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.