Байесовские сети как инструмент поддержки принятия решений в условиях неопределённости, страница 6

Вершины решений содержат перечень альтернатив, комбинации которых задают общее дерево решений. Временнóе старшинство при этом задаётся дугами сети:

- стрелка от вершины шансов к вершине решения означает, что состояние случайной переменной известно на момент принятия  решения;

- стрелка от переменной решения к какой-либо другой переменной указывает, что принятое решение влияет на состояния случайной переменной или на значения локальной функции полезности.

При этом сеть должна оставаться без контуров, а для реализации в Hugin Lite ещё и требуется, чтобы в сети обязательно существовал путь, содержащий все вершины решений.

Прямое назначение диаграмм влияния ― поддержка принятия решений в условиях неопределённости.

Процесс принятия решения с использованием диаграмм влияния будет осуществляться  следующим образом:

- после наблюдения значений случайных переменных, которые являются родителями первой вершины решения, вычисляется максимальная полезность для альтернатив в предположении, что с учётом всех свидетельств, имеющихся на момент принятия каждого решения, все будущие решения окажутся оптимальными;

- выбираем альтернативу, при которой ожидаемая полезность максимальна;

- по мере развития процесса аналогичные действия выполняем для следующей вершины решений.

В расчёте используются те же методы, что и в БСД, для чего вершины решения замещаются вершинами шансов. Вычисление ожидаемой полезности при выборе альтернатив базируется на положениях динамического программирования.

Содержание работы

1. Изучение диаграмм влияния в среде ИЭС Hugin Lite на показательных примерах.

Пример 1. Рассмотрим небольшую задачу поддержки принятия решений из области нефтеразведки, формализованную в виде диаграммы влияния, представленной на рис. 2.1.

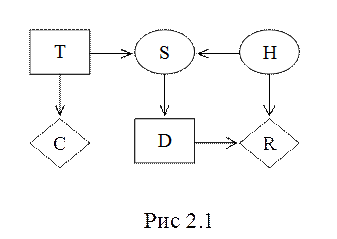Нефтяники должны принять решение D о бурении скважины. Предварительная экспертиза геологов выявила вероятности состояний нефтяного пласта H, а эксперты оценили размеры прибыли или убытка R в зависимости от конкретного состояния пласта. Дополнительную информацию о состоянии месторождения могут дать результаты сейсмотеста S (может дать однозначно закрытую структуру, открытую или отсутствие геологической структуры), проведение которого стоит C. Требуется принять решение T: целесообразно ли проводить сейсмотест.

Имеются следующие количественные характеристики. Вероятности состояний пласта: p(H = «dk») = 0.5 ― сухой, p(H = «wt») = 0.3 ― влажный, p(H = «sk») = 0.2 ― мокрый. Вероятности выхода сейсмотеста в зависимости от состояний пласта при проведении сейсморазведки приведены в табл. 2.1. При непроведении сейсморазведки считаем, что все состояния переменной S равновероятны. Стоимость сейсморазведки составляет $10 тыс. Ожидаемый доход от бурения с мокрого пласта должен составить $200 тыс., с влажного ― $50 тыс., а с сухого ― убыток $70 тыс.

Таблица 2.1

Загрузите эту диаграмму влияния из файла «oil.net», ознакомьтесь с ней и перейдите в режим исполнения. В списке слева будут представлены вершины шансов и вершины полезности. Видим, что для вершины T математическое ожидание полезности при проведении сейсморазведки составит $22.5 тыс., а при непроведении ― $20 тыс. Таким образом, по критерию максимума математического ожидания полезности выгодно проводить сейсморазведку. Зафиксируем принятие решения о проведении разведки и введём этот факт как свидетельство. Теперь оценки полезности для вершины D уменьшились на 10 ед. Посмотрим, какова будет величина математического ожидания полезности при каждом из результатов теста. Убеждаемся, что при отсутствии структуры (S = «di») диаграмма влияния показывает отрицательное математическое ожидание полезности (– 40.49) и, следовательно, лучше не бурить, потеряв $10 тыс., чем бурить с большой вероятностью риска (0.7317) потерять $70 тыс. При благоприятных же результатах риск составит соответственно 0.21 (закрытая структура) и 0.43 (открытая). В то же время без разведки, опираясь только на мнение экспертов, имеем математическое ожидание полезности, равное $20 тыс. (0.2·200 + + 0.32·50 – 0.5·70), и риск убытка в размере $70 тыс. с вероятностью 0.5.