Monte Carlo simulation of colloidal membrane filtration: Model development with application to characterization of colloid phase transition, страница 9

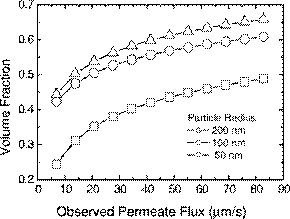
Fig. 8. Cake layer volume fraction in relation to observed permeate flux with varying particle radius. The following parameters (in addition to those listedinTable1)wereusedinthesimulations:zetapotential=−30mV,ionic strength=10−₃ M.

in Eqs. (10)–(12). This model relies on using a linear superposition approximation with constant potential. Rigorous derivation and defense of this method are given in Bell et al. [25] and Chew and Sen [26].

Otherexpressionsforelectrostaticdoublelayerinteraction are available. Among them are the fundamental expressions for interactions at constant surface potential, constant surface charge, and many more other models [3,38]. A thorough discussion of the various options available is given in Chen and Kim [8].

The choice of models bears significant consequences. To further illustrate this point, a parameter R is introduced to gaugetherelativemagnitudeofthedownwardhydrodynamic drag versus the inter-particle electrostatic potential:

                                                                     (20)

where V_s is the difference in inter-particle potentials measured at a particle separation of 2.5 times particle radius, with a displacement r of 0.1 times particle radius. Eq. (20) essentially measures the ratio of the hydrodynamic force that the particle experiences while displacing 0.1 times particle radius in the negative z-direction towards another particle 2.5 times particle radius away versus the resistance against this displacement from the inter-particle repulsion.

Fig. 9 shows the particle volume fraction as a function of the logarithm of R. The curves exhibit two distinct regions. In region I, the particle volume fraction is an increasing function of logR. This is an expected trend and signifies that a greater hydrodynamic drag will compress the particle configuration and generate a higher volume fraction. The model implemented in the current study according to Eqs. (10)–(12) does in fact fall within region I as supported by results given in Figs. 4, 5 and 8. However, in region II, the volume fraction becomes a decreasing function of logR. In this case, the hydrodynamic drag has surpassed a threshold beyond which it is so strong relative to the inter-particle potential that particles coalesce rapidly with less opportunity to reorder or re-

Fig. 9. Sensitivity of cake layer volume fraction to the relative magnitudes of hydrodynamic drag force vs. inter-particle potential. The following parameters (in addition to those listed in Table 1) were used in the simulations: (a) ionic strength=10−¹, (b) ionic strength=10−².

structure their configuration. As a result, the volume fraction decreases with increasing hydrodynamic drag. Switching to a different model for the inter-particle potential or varying the magnitude of the physical parameters inputted into the model may cause the model to shift from region I to region II or vice versa.

Fig. 9(a) and (b) also shows a comparison of the behavior of the ratio logR in response to adjustments in the ionic strength. With a lower ionic strength of 10−² M in Fig. 9(b), the values of logR decrease significantly from that of Fig. 9(a). This is because at a lower ionic strength, inter-particle repulsive interactions are stronger and therefore greatly reduces the ratio of hydrodynamic force versus inter-particle repulsion. Nevertheless, even when the interparticle repulsions are stronger, a threshold still exists where the particle deposition dynamics will transition into a region II behavior as shown in Fig. 9(b).