Forfiltrationofpolydispersesuspensions,onebeliefabout the polydisperse particle size distribution states that the smaller particles will occupy void spaces between the larger onesandtherebyincreasetheoverallvolumefraction[34,35]. However, this notion should be conditioned by the observation that particles of various sizes will experience different hydrodynamic drag forces. So, the deposition dynamics of particles will vary according to the particle sizes. Therefore, the possibility exists that within the cake layer there may be a disproportionate particle size distribution that is different from the distribution in the bulk phase. Instead of the situation with void-filling by smaller particles, the cake layer may exhibit a stratification with respect to particle size where the larger particles are abundant throughout and smaller parti-
|
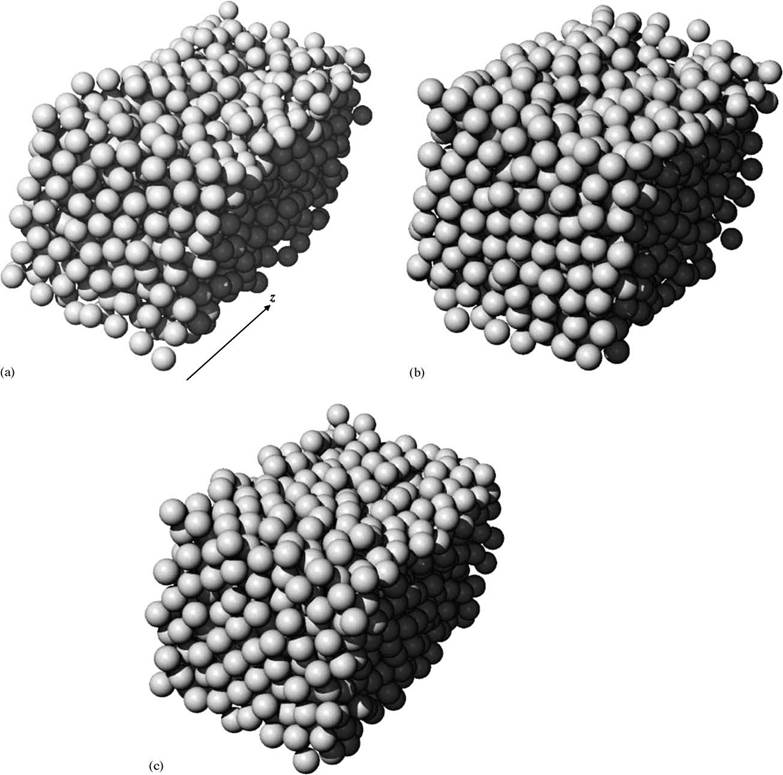
Fig. 6. Illustrations of final particle configurations. (a) Observed permeate flux=6.9m/s, particle radius=100nm, ionic strength=10−3 M, zeta potential=−30mV, volume fraction=0.423, average center-to-center inter-particle spacing=2.250 times particle radius. (b) Observed permeate flux =27.6m/s, particle radius=100nm, ionic strength=10−3 M, zeta potential=−30mV, volume fraction=0.527, average inter-particle spacing=2.075 times particle radius. (c) Observed permeate flux=82.8m/s, particle radius=100nm, ionic strength=10−3 M, zeta potential=−30mV, volume fraction=0.608, average |
 |
cles deposit mostly near the top portions of the cake layer. Now the smaller particles contribute not a void-filling effect but only a higher specific resistance within a certain concentrated region in the cake layer.
In addition, complications will arise in crossflow filtration of polydisperse particles. Here, the larger particles will experience greater hydrodynamic drag from the crossflow and be more susceptible to re-entrainment back into the bulk. The tendency for the larger particles to re-entrain will work against its faster downward velocity. So, once again, the situation portrays a complex counteraction between two hydrodynamic drag forces, permeation and crossflow, both of which are functions of a polydisperse particle distribution. This may then explain the contradictory findings intimated in some studies that the crossflow functions to reduce the permeateflux[11,36]whenthetraditionalviewcontendsjustthe opposite. Thus, a macroscopic generalization of the system response to variations in particle sizes is open to exceptions
|
Fig. 7. Illustrations of final particle configurations. (a) Observed permeate flux=6.9m/s, particle radius=100nm, ionic strength=10−3 M, zeta potential=−90mV, volume fraction=0.331, average center-to-center inter-particle spacing=2.450 times particle radius. (b) Observed permeate flux=27.6m/s, particle radius=100nm, ionic strength=10−3 M, zeta potential=−90mV, volume fraction=0.401, average inter-particle spacing=2.250 times particle radius. (c) Observed permeate flux=82.8m/s, particle radius=100nm, ionic strength=10−3 M, zeta potential=−90mV, volume fraction=0.456, average |
 |
as those observed in Mackley and Sherman [11,36]. But, a microscopic model such as MC simulation is sufficiently robust to capture such anomalies by rigorously computing each individual particle trajectory.
Figs. 4, 5 and 8 have clearly demonstrated the considerable impact of the hydrodynamic drag and inter-particle potential on the eventual cake layer volume fraction. Therefore, the selection of models for these two quantities should be undertaken with diligence and scrutiny. Modeling the hydrodynamic drag force by Stokes law as given in Eq. (13) is historically proven and established to be correct [37]. So, attention now shifts to the inter-particle interaction, which remains an open question in terms of how to accurately model the van der Waals and electrostatic potentials. In this study, the model for the inter-particle electrostatic potential is given
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.