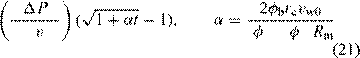Monte Carlo simulation of colloidal membrane filtration: Model development with application to characterization of colloid phase transition, страница 11

5.2.  Relating critical flux to phase transition

Adead-endfiltrationsystem,showninFig.1,willbemodeled here. No crossflow shear occurs in the dead-end system. The only forces present are the applied pressure and interparticle potential. For this case, a system of equations is first solved, Eq. (5) and the two equations [31]: δc ⁼          −

              µrc w0                                                                 ( c           b)

Solving this set of equations will yield the system response of permeate flux as a function of applied pressure, shown in Fig. 10. For a dead-end filtration system, the particle deposit will continually build up over time, and so the system response will also vary with time of filtration (2 and 5h). At 5h, a thicker cake layer has accumulated and so the yield in permeate flux is lower than after 2h of filtration.

The two forms of the critical flux are identifiable from the curves in Fig. 11. The strong form of the critical flux occurs at low applied pressures as the system response deviates from the clean water flux. For the case of 10−³ M ionic strength and 5h of filtration, the strong form of the critical flux occurs at applied pressure of 6.894kPa (1psi) (Fig. 11(a)). The volume fraction of the cake layer is 0.472 with thickness

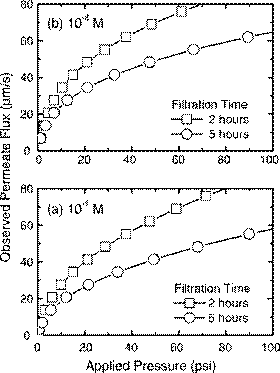
Fig. 10. Observed permeate flux as a function of applied pressure for 2 and 5h of dead-end filtration. The following parameters (in addition to those listed in Table 1) were used in the simulations: (a) zeta potential=potential=−30mV, ionic strength−30mV, ionic strength=10−=10¹ M, particle radius=100nm; (b) zeta−_{3 M, particle radius=100nm.}

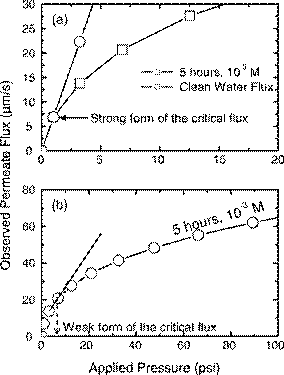
Fig. 11. Identification of the strong form of the critical flux. The following parameters (in addition to those listed in Table 1) were used in the simulations: (a) zeta potential=−30mV, ionic strength=10−³ M, particle radius=100nm. The volume fraction of the cake layer at the strong form of the critical flux is 0.472 with cake thickness 28.6m and average center-tocenter inter-particle separation distance of 2.250 times particle radius; (b) zeta potential=−30mV, ionic strength=10−³ M, particle radius=100nm. The volume fraction of the cake layer at the weak form of the critical flux is 0.537 with cake thickness 136m and average inter-particle separation 2.195 times particle radius.

28.6m and average center-to-center inter-particle separation distance of 2.25 times particle radius. There is very little basis to assign the strong form of the critical flux as the point of phase transition. First, the particles are not in contact. Second, the particle deposit does not greatly affect the system behavior (only the beginning of a deviation from the clean water flux is observed). The strong form of the critical flux fails on both fronts, the simplistic view of phase transition in terms of particle contact and the practical view in terms of operational impact. Therefore, the strong form of the critical flux only defines the presence of a fluid-like polarized layer (i.e., concentration polarization).

From Fig. 11(b), the weak form of the critical flux for the case of 10−³ M ionic strength occurs at 55.152kPa (8psi) applied pressure with volume fraction 0.537, cake thickness 136m, and average center-to-center inter-particle separation 2.195 times particle radius. Here again the particles are not in contact. However, a significant change in filtration behavior does occur. Once the system diverges from the linear relationship beyond the weak form of the critical flux, the filtration performance begins to decline greatly. As can be seen from Fig. 10(a) and (b), a large increase in the applied pressure after the critical flux will no longer generate nearly the comparable increase in flux as prior to the critical flux. This deterioration in productivity caused by the cake layer is commonly termed membrane fouling. It would then be appropriate to designate this to be another possible point of phase transition. The weak form of the critical flux demarcates the onset of phase transition from concentration polarization to a particle deposit that will substantially restrict filtration performance. The particles need not be in contact; the underpinning criterion adopts a practical consideration where an incremental increase in the applied pressure will yield only limited increase in permeate flux. The rationale behind this perspective argues that the transition from a fluid to solid phase should be defined in terms of the impact on filtration performance. Once a significant decline in filtration productivity is observed, the solidification of the cake layer is deemed to occur. A summary of the strong and weak forms of the critical flux for the case of ionic strength 10−³ M is given in Fig. 12.