Monte Carlo simulation of colloidal membrane filtration: Model development with application to characterization of colloid phase transition, страница 5

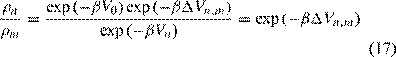
where β =1/k_BT. In this procedure, a uniform random number between 0 and 1, ξ, is generated and compared with

), then the uphill move

is accepted. Otherwise the proposed move is rejected for

). The overall effect is that the particle proceeds with changes in potential energy V_n,m accepted with probability exp(). If the uphill move is rejected, the particle remains in its original position, and the non-move is taken to be a new state nevertheless.

The modeling procedure continues by randomly selecting successive particles for proposed displacements and evaluating each move. Hastings [29] presents an equally valid method of selecting particles systematically according to their indices rather than by random selection. This step eases the number of random number generations. For the Hastings method, an important distinction should be noted, and that is it does not satisfy detailed balance. Manousiouthakis and Deem [30] prove that the Hastings method only satisfies balance. Details of Monte Carlo modeling are given in Allen and Tildesley [9].

3.2.  Hydrodynamic bias Monte Carlo simulationalgorithm for colloidal membrane filtration

The model in the current study utilizes a rectangular simulation box containing 1024 particles. The algorithm for the simulation follows the method described in Section 3.1. Individual particles are assigned random proposed displacement with subsequent evaluation of the energy change of each move. Downhill moves ( <0) are readily accepted while uphill moves are subject to the probability test given in Eq. (17).

A preliminary MC simulation is first performed to obtain an equilibrium configuration for the particles. Details of this procedure are given in Kim and Hoek [31]. Upon reaching an equilibrium configuration, the simulation proceeds to model particle motion under the influences of hydrodynamic drag and inter-particle interaction potential. It is important to note here that the particles should be displaced solely in one of the three orthogonal directions (x, y, and z only) for each energy evaluation (Fig. 3). This stipulation ensures that forces acting in a perpendicular direction to the proposed particle

Fig. 3. Sequence of particle displacements during Monte Carlo simulation.

displacement will not affect that particular particle move. So, the hydrodynamic drag force, which acts in the downward z-direction, will only come into play when particles are displaced solely in the z-direction and will not influence particle motion in the x- or y-directions only. Such a vectorial decompositionoffersfasterconvergencetothedynamicequilibrium ofthesystem.Therandomnessofthedisplacementselections is maintained to be almost identical to the case without the decomposition. This procedure results in a mean field hydrodynamic bias MC method.

When particles are displaced in the x or y directions only, the expression for the energy evaluation is

,NEW − VTOT,OLD                                                      (18)

where the total inter-particle interaction energy V_TOT is computed according to Eqs. (8)–(12). The added subscripts NEW and OLD signify total inter-particle energy computed at the proposed displacement location and at the original particle location, respectively.

Particle displacements in the z-direction only will acquire an additional term in the energy evaluation due to the downward hydrodynamic drag force. The expression for the difference in energy then becomes:

,NEW − VTOT,OLD + FStokesΩ(znew − zold)

(19)

wherez_new andz_old arethezcoordinatesofparticlesattheproposed displacement and original locations, respectively. For particle motion in the z-direction, there is no cyclic boundary condition occurring at the membrane surface. Particles are not allowed to move below z=0. For cases involving a cyclic boundary condition, the simulation step must maintain balance [9,30]. The simulation proceeds with individual particle displacements followed by energy evaluations according to Eqs. (18) and (19) until reaching a final dynamic equilibrium particle configuration. The criterion for ascertaining equilibration of the system is that the volume fraction of the cake layer and average inter-particle separation between a pair of nearestparticlesreachasteadystateandremainconstantcontinuously after that point. Details of this bias Monte Carlo technique are verified and well discussed in Kim et al. [32].