Fig. 4 shows the model results that simulate the deposition of particles at the membrane surface under the coupled influences of hydrodynamic drag and inter-particle electrostatic interaction. The specific input parameters used in these simulations are given in Table 1. In Fig. 4, the volume fraction of the particle deposit is given as a function of observed permeate flux of the filtration system. In these simulations, a
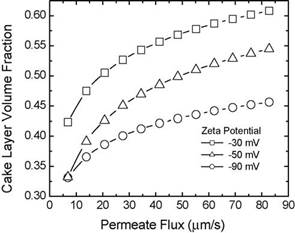
Fig. 4. Cake layer volume fraction in relation to permeate flux with varying zeta potential. The following parameters (in addition to those listed in Table 1) were used in the simulations: particle radius=100nm, ionic strength=10−3 M.
permeatefluxisfirstsettoaselectedvalue.Then,theeffective permeate flux within the cake layer is adjusted for the volume fraction of the porous medium according to Eq. (12) to yield the actual hydrodynamic drag force experienced by the particles. The model utilizes the adjusted hydrodynamic drag force along with the inter-particle potential to simulate particle deposition and the final cake configuration. Each curve in Fig. 4 essentially shows the increase in volume fraction of particleswithincreasingcompressiveforcefromtheadjusted hydrodynamic drag. For instance, at −30mV zeta potential, the cake layer volume fraction increases from 0.423 to 0.608 with corresponding increases in the observed permeate flux from 6.9 to 82.8m/s. Conversely, increasing the particle zeta potential effectively strengthens the inter-particle electrostatic repulsion and prevents particles from closely approaching one another (low volume fraction). At zeta potential of −90mV, the cake layer attains a volume fraction of only0.456atobservedpermeatefluxof82.8m/s,contrasted to a much greater volume fraction of 0.608 for −30mV.
Similar trends are shown in Fig. 5 for cake layer formation under various solution ionic strengths. Like the zeta potential, the solution ionic strength governs the magnitude and range of the inter-particle electrostatic interaction. At high ionic strength, excess electrolyte ions screen the interparticle interactions and lessen the inter-particle repulsion. For instance, at an ionic strength of 10−2 M, the cake layer volume fraction is shown to be consistently higher than that for 10−4 M. However, it is interesting to note that, for all three ionic strengths at observed permeate flux 82.8m/s, the cake layer volume fractions converge to a value of apTable 1
Operating and system conditions for model simulations
![]()
Hamaker constant, AH (J) 4.6×10−21
Valence of ions, zs 1
Dielectric permittivity of water 78.54
Permittivity of free space (C2/Nm2) 8.854×10−12
Temperature (K) 298.5
![]() Membrane resistance (1/m) 1×1012
Membrane resistance (1/m) 1×1012
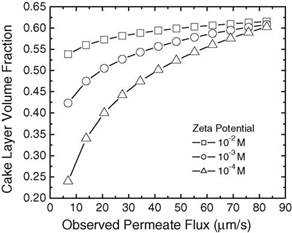
Fig. 5. Cake layer volume fraction in relation to permeate flux with varying solution ionic strength. The following parameters (in addition to those listed in Table 1) were used in the simulations: particle radius=100nm, zeta potential=−30mV.
proximately 0.6, the random loose packing ratio according to Onoda and Liniger [33]. The hydrodynamic drag dominates the influence from the ionic strength at this point. The results of Figs. 4 and 5 demonstrate the model’s capacity to successfully capture the compelling and contrary impact of hydrodynamic drag and inter-particle electrostatic interaction on cake layer formation. Comparison of Figs. 4 and 5 reveals that the zeta potential serves as a stronger differentiating agent over the ionic strength for cake formation dynamics at high permeate flux as the profound impact of zeta potential remains clearly evident at high permeate flux.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.